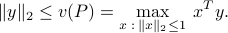Cauchy-Schwartz Inequality
For any two vectors 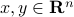 , we have
, we have

The above inequality is an equality if and only if 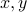 are collinear. In other words:
are collinear. In other words:
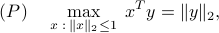
with optimal  given by
given by 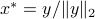 if
if 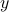 is non-zero.
is non-zero.
Proof: The inequality is trivial if either one of the vectors 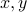 is zero. Let us assume both are non-zero. Without loss of generality, we may re-scale
is zero. Let us assume both are non-zero. Without loss of generality, we may re-scale  and assume it has unit Euclidean norm (
and assume it has unit Euclidean norm (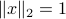 ). Let us first prove that
). Let us first prove that
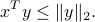
We consider the polynomial
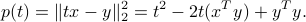
Since it is non-negative for every value of 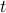 , its discriminant
, its discriminant  is non-positive. The Cauchy-Schwartz inequality follows.
is non-positive. The Cauchy-Schwartz inequality follows.
The second result is proven as follows. Let 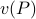 be the optimal value of the problem. The Cauchy-Schwartz inequality implies that
be the optimal value of the problem. The Cauchy-Schwartz inequality implies that  . To prove that the value is attained (it is equal to its upper bound), we observe that if
. To prove that the value is attained (it is equal to its upper bound), we observe that if 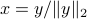 , then
, then
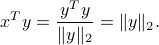
The vector 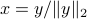 is feasible for the optimization problem
is feasible for the optimization problem 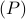 . This establishes a lower bound on the value of
. This establishes a lower bound on the value of 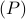 ,
, 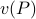 :
: