Fundamental theorem of linear algebra

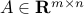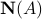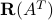Let $A in mathbf{R}^{m times n}$ . The sets mathbf{N} (A) and $mathbf{R} (A^T)$ form an orthogonal decomposition of 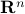$mathbf{R}^n$ , in the sense that any vector $x in mathbf{R}^n$ can be written as

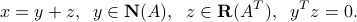
$x = y + z, ;; y in mathbf{N} (A), ;; z in mathbf{R} (A^T), ;; y^Tz = 0.$

In particular, we obtain that the condition on a vector to be orthogonal to any vector in the nullspace of implies that it must be in the range of its transpose:

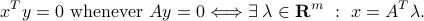
$x^Ty = 0 mbox{ whenever } Ay = 0 Longleftrightarrow exists : lambda in mathbf{R}^m ~:~ x = A^Tlambda.$

Proof: The theorem relies on the fact that if a SVD of a matrix is

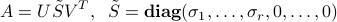
$A = U tilde{ {S}} V^T, ;; tilde{ {S}} = mbox{bf diag}(sigma_1,ldots,sigma_r,0,ldots,0)$

then an SVD of its transpose is simply obtained by transposing the three-term matrix product involved:

$A^T = (U tilde{ {S}} V^T)^T = V tilde{S} U^T.$

Thus, the left singular vectors of are the right singular vectors of A^T .

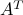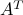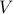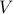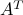From this we conclude in particular that the range of A^T is spanned by the first columns of . Since the nullspace of is spanned by the last n-r columns of , we observe that the nullspace of and the range of A^T are two orthogonal subspaces, whose dimension sum to that of the whole space. Precisely, we can express any given vector in terms of a linear combination of the columns of 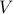; the first columns correspond to the vector $z in mathbf{R}(A^T)$ and the last n-r to the vector y in mathbf{N}(A) :

$x = V(V^Tx) = underbrace{sum_{i=1}^r tilde{x}_i v_i}_{=z} + underbrace{sum_{i=r+1}^n tilde{x}_i v_i}_{=y}, ;; tilde{x} := V^Tx.$

This proves the first result in the theorem.

The last statement is then an obvious consequence of this first result: if is orthogonal to the nullspace, then the vector 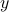in the theorem above must be zero, so that $x in mathbf{R}(A^T)$ .