Dimension of hyperplanes
A set 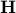 in
in 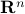 of the form
of the form
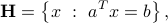
where 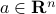 ,
, 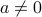 , and
, and 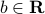 are given, is an affine set of dimension
are given, is an affine set of dimension  .
.
Conversely, any affine set of dimension  can be represented by a single affine equation of the form
can be represented by a single affine equation of the form 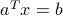 , as in the above.
, as in the above.
Proof:
Consider a set
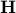 described by a single affine equation:
described by a single affine equation:

with 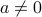 . Let us assume for example that
. Let us assume for example that  . We can express
. We can express 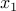 as follows:
as follows:

This shows that the set is of the form  , where
, where

Since the vectors  are independent, the dimension of
are independent, the dimension of 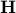 is
is  . This proves that
. This proves that 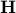 is indeed an affine set of dimension
is indeed an affine set of dimension  .
.
The converse is also true. Any subspace
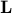 of dimension
of dimension  can be represented via an equation
can be represented via an equation  for some
for some 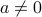 . A sketch of the proof is as follows. We use the fact that we can form a basis
. A sketch of the proof is as follows. We use the fact that we can form a basis  for the subspace
for the subspace 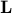 . We can then construct a vector
. We can then construct a vector  that is orthogonal to all of these basis vectors. By definition,
that is orthogonal to all of these basis vectors. By definition, 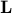 is the set of vectors that are orthogonal to
is the set of vectors that are orthogonal to  .
.