Rank-nullity theorem

The nullity (dimension of the nullspace) and the rank (dimension of the range) of a 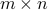m times n matrix add up to the column dimension of , .

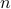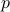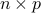Proof: Let be the dimension of the nullspace mathbf{N}(A) ( p le n ). Let U_1 be a n times p matrix such that its columns form an orthonormal basis of . In particular, we have AU_1 = 0 . Using the QR decomposition of the matrix $[U_1,I_{n}]$ we obtain a n times (n-p) matrix U_2 such that the matrix [U_1,U_2] is orthogonal. Now define the m times (n-p) matrix V := AU_2 .

We proceed to show that the columns of 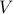form a basis for the range of . To do this, we first prove that the columns of 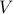span the range of . Then we will show that these n-p columns are independent. This will show that the dimension of the range (that is, the rank) is indeed equal to n-p .

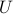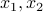Since is an orthonormal matrix, for any $x in mathbf{R}^n$ , there exist two vectors x_1,x_2 such that x = U_1x_1+U_2x_2 . If x in mathbf{R}(A) , then $Ax = AU_2x_2 = Vx_2 in mathbf{R}(V)$ . This proves that the columns of 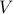span the range of : mathbf{R}(A) = mathbf{R}(V) .

Now let us show that the columns of 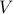are independent. Assume a vector satisfies Vz = 0 , and let us show z=0 . We have Vz=AU_2 z = 0 , which implies that U_2z is in the nullspace of . Hence there exist another vector 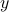such that U_2z = U_1y . This is contradicted by the fact that [U_1,U_2] is an orthogonal matrix: pre-multiplying the last equation by U_2^T , and exploiting the fact that $U_2^TU_2 = I_{n-p}$ , U_2^TU_1 = 0 , we obtain z = U_2^TU_2 z = U_2^TU_1 y = 0 .