Spectral theorem: eigenvalue decomposition for symmetric matrices

Spectral theorem

We can decompose any symmetric matrix $A in mathbf{S}^n$ with the symmetric eigenvalue decomposition (SED)

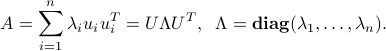
$A = sum_{i=1}^n lambda_i u_iu_i^T = U Lambda U^T, ;; Lambda = mbox{bf diag}(lambda_1,ldots,lambda_n) .$

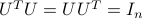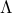where the matrix of U := [u_1 , ldots, u_n] is orthogonal (that is, U^TU=UU^T = I_n ), and contains the eigenvectors of , while the diagonal matrix Lambda contains the eigenvalues of .

Proof: The proof is by induction on the size

of the matrix

. The result is trivial for n = 1

. Now let

and assume the result is true for any matrix of size n-1

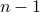Consider the function of

. From the basic properties of the determinant, it is a polynomial of degree

, called the characteristic polynomial of

. By the fundamental theorem of algebra, any polynomial of degree

has

(possibly not distinct) complex roots; these are the called the eigenvalues of

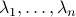. We denote these eigenvalues by lambda_1,ldots,lambda_n

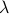is an eigenvalue of

, that is, det(lambda I - A) = 0

, then

must be non-invertible (see here). This means that there exist a non-zero real vector

such that

. We can always normalize

so that

. Thus,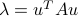

is real. That is, the eigenvalues of a symmetric matrix are always real.

Now consider the eigenvalue lambda_1

and an associated eigenvector u_1

. Using the Gram-Schmidt orthogonalization procedure, we can compute a n times (n-1)

matrix

such that

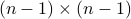is orthogonal. By induction, we can write the (n-1) times (n-1)

symmetric matrix V_1^TAV_1

, where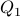

is a

matrix of eigenvectors, and $Lambda_1 = mbox{bf diag}(lambda_2,ldots,lambda_n)$ are the n-1

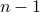eigenvalues of V_1^TAV_1

. Finally, we define the n times (n-1)

matrix

. By construction the matrix U := [u_1,U_1]

is orthogonal.

$U^TAU = left( begin{array}{c} u_1^T U_1^T end{array}right)A left( begin{array}{cc} u_1 & U_1 end{array}right) = left( begin{array}{cc} u_1^TAu_1 & u_1^TAU_1 U_1^TAu_1 & U_1^TAU_1 end{array}right) = left( begin{array}{cc} lambda_1 & 0 0 & Lambda_1 end{array}right) ,$

We have exhibited an orthogonal 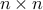n times n

matrix

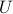such that

is diagonal. This proves the theorem.