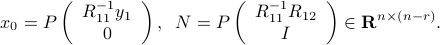Set of solutions to the least-squares problem via QR decomposition
The set  of solutions to the least-squares problem
of solutions to the least-squares problem
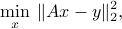
where  , and
, and 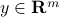 are given, can be expressed in terms of the full QR decomposition of
are given, can be expressed in terms of the full QR decomposition of  :
:
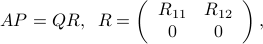
where 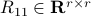 is upper triangular and invertible,
is upper triangular and invertible, 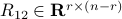 ,
, 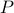 is a permutation matrix, and
is a permutation matrix, and 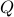 is
is 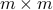 and orthogonal.
and orthogonal.
Precisely we have 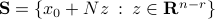 , with
, with 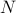 a matrix whose columns span the nullspace of
a matrix whose columns span the nullspace of  :
:
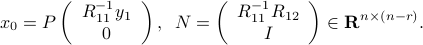
Proof: Since  and
and  are orthogonal, we have, with
are orthogonal, we have, with 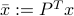 ,
, 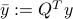 :
:
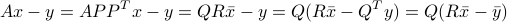
Exploiting the fact that 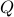 leaves Euclidean norms invariant, we express the original least-squares problem in the equivalent form:
leaves Euclidean norms invariant, we express the original least-squares problem in the equivalent form:
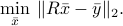
Once the above is solved, and 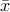 is found, we recover the original variable
is found, we recover the original variable  with
with 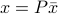 .
.
Now let us decompose 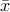 and
and 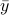 in a manner consistent with the block structure of
in a manner consistent with the block structure of 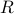 :
: 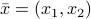 ,
, 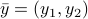 , with
, with 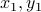 two
two  -vectors. Then
-vectors. Then
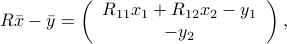
which leads to the following expression for the objective function:
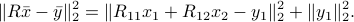
The optimal choice for the variables 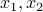 is to make the first term zero, which is achievable with
is to make the first term zero, which is achievable with
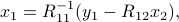
where 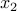 is free, and describes the ambiguity in the solution. The optimal residual is
is free, and describes the ambiguity in the solution. The optimal residual is 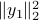 .
.
We are essentially done: with 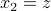 , we can write
, we can write
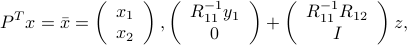
that is: 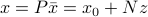 , with
, with