Backwards substitution for solving triangular linear systems

Consider a triangular system of the form 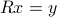Rx = y , where the vector 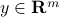$y in mathbf{R}^m$ is given, and 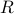is upper-triangular.

Let us first consider the case when 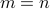m=n , and 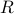is invertible. Thus, 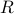has the form

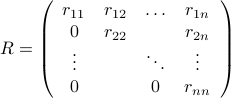
$R = left( begin{array}{cccc}r_{11} & r_{12} & ldots & r_{1n} 0 & r_{22} & & r_{2n} vdots & & ddots & vdots 0 & & 0 & r_{nn} end{array}right)$

with each 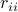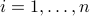$r_{ii}$ , i=1,ldots,n non-zero.

The backwards substitution first solves for the last component of using the last equation:

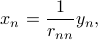
$x_n = frac{1}{r_{nn}} y_n ,$

and then proceeds with the following recursion, for 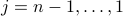j=n-1,ldots,1 :

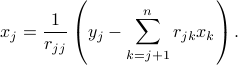
$x_j = frac{1}{r_{jj}} left( y_j - sum_{k=j+1}^n r_{jk} x_k right) .$

Example: Solving a 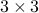3 times 3 triangular system by backwards substitution