Pseudo-Inverse of a Matrix
The pseudo-inverse of a 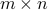 matrix
matrix  is a matrix that generalizes to arbitrary matrices the notion of inverse of a square, invertible matrix. The pseudo-inverse can be expressed from the singular value decomposition (SVD) of
is a matrix that generalizes to arbitrary matrices the notion of inverse of a square, invertible matrix. The pseudo-inverse can be expressed from the singular value decomposition (SVD) of  , as follows.
, as follows.
Let the SVD of  be
be

where 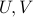 are both orthogonal matrices, and
are both orthogonal matrices, and 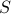 is a diagonal matrix containing the (positive) singular values of
is a diagonal matrix containing the (positive) singular values of  on its diagonal.
on its diagonal.
Then the pseudo-inverse of  is the
is the 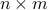 matrix defined as
matrix defined as

Note that 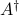 has the same dimension as the transpose of
has the same dimension as the transpose of  .
.
This matrix has many useful properties:
If
 is full column rank, meaning
is full column rank, meaning  , that is,
, that is, 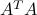 is not singular, then A
is not singular, then A is a left inverse of
is a left inverse of  , in the sense that
, in the sense that 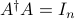 . We have the closed-form expression
. We have the closed-form expression

If
 is full row rank, meaning
is full row rank, meaning  , that is,
, that is, 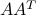 is not singular, then A
is not singular, then A is a right inverse of
is a right inverse of  , in the sense that
, in the sense that 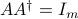 . We have the closed-form expression
. We have the closed-form expression
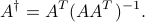
If
 is square, invertible, then its inverse is
is square, invertible, then its inverse is  .
.The solution to the least-squares problem
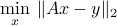
with minimum norm is 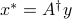 .
.
Example: pseudo-inverse of a 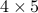 matrix.
matrix.