Optimization Models
Home
Software
Links
Index
Contact
1. Introduction
1.1. Overview
1.2. Optimization Models
2. Linear Algebra
2.1. Vectors
2.2. Matrices
2.3. Linear Equations
2.4.  Least-Squares
2.5. Eigenvalues
2.6  Singular Values
3. Convex Models
3.1. Convexity
3.2. LP and QP
3.3. SOCP
3.4. Robust LP
3.5. GP
3.6. SDP
3.7. Non-Convex Models
4. Duality
4.1. Weak Duality
4.2. Strong Duality
4.3.  Applications
5. Case Studies
5.1. Senate Voting
5.2. Antenna Arrays
5.3. Localization
5.4. Circuit Design

Proving convexity via monotonicity

Consider the function 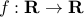f : mathbf{R} rightarrow mathbf{R}, with values f(x) = x^4.

We can express the function as the composition of the function

g(x) = x^2

with the function 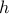h with values

h(y) = left{ begin{array}{ll} y^2 & mbox{if } y ge 0 +infty & mbox{otherwise.} end{array} right.

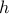That is, f(x) = h(g(x)). Since g(x) belongs to the domain of h for every x in mathbf{R}, the domain of f is indeed the whole real line.

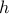The functions g,h are both convex, and h is monotone increasing (note that the domain of 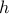h is chosen to ensure monotonicity). Hence, by the monotonicity property, the composition 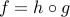f = h circ g is also convex.

alt text 

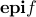The picture shows the set { (x,y,z) ::: h(y) le z, ;; g(x) le y } (in three dimensions), and its projection on the space of (x,z)-variables, which is the epigraph of f, mbox{bf epi} f. The epigraph of 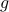g is the projection of the same set on the space of (x,y)-variables.