Convex Functions
Definition
Alternate characterizations of convex functions
Operations that preserve convexity:
Composition with an affine function
Point-wise maximum
Nonnegative weighted sum
Partial minimum
Composition with monotone convex functions
Definition
Domain of a function
The domain of a function 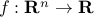 is the set
is the set 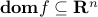 over which
over which  is well-defined, in other words:
is well-defined, in other words:
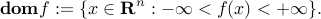
Here are some examples:
The function with values
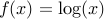 has domain
has domain 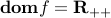 .
.The function with values
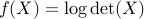 has domain
has domain 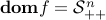 (the set of positive-definite matrices).
(the set of positive-definite matrices).
Definition of convexity
A function 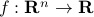 is convex if
is convex if
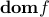 is convex;
is convex;In addition,
![forall, x_1,x_2 in mbox{bf dom} f, ;; forall, theta in [0, 1], f left(theta x + (1-theta) yright) le theta f(x) + (1-theta) f(y) .](eqs/9018258276193511749-130.png)
Note that the convexity of the domain is required. For example, the function 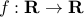 defined as
defined as
![f(x) = left{ begin{array}{ll} x & mbox{if } x notin [-1,1] +infty & mbox{otherwise} end{array}right.](eqs/3707423515173210456-130.png)
is not convex, although is it linear (hence, convex) on its domain ![]-infty,-1)cup(1,+infty[](eqs/4406577851778482381-130.png) .
.
We say that a function is concave if 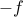 is convex.
is convex.
Examples:
The function
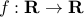 defined as
defined as 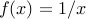 for
for 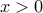 and
and 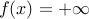 for
for 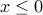 is convex. However, the function with domain the whole line except
is convex. However, the function with domain the whole line except 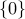 is not, since that domain is not convex.
is not, since that domain is not convex.
Alternate characterizations of convexity
Let 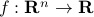 . The following are equivalent conditions for
. The following are equivalent conditions for  to be convex.
to be convex.
Epigraph
A function 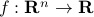 is convex if and only if its epigraph
is convex if and only if its epigraph
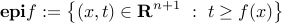
is convex.
Example: We can us this result to prove for example, that the largest eigenvalue function 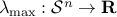 , which to a given
, which to a given 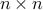 symmetric matrix
symmetric matrix 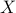 associates its largest eigenvalue, is convex, since the condition
associates its largest eigenvalue, is convex, since the condition 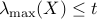 is equivalent to the condition that
is equivalent to the condition that 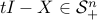 .
.
First-order condition
If  is differentiable (that is,
is differentiable (that is, 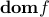 is open and the gradient exists everywhere on the domain), then
is open and the gradient exists everywhere on the domain), then  is convex if and only if
is convex if and only if
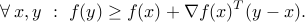
The geometric interpretation is that the graph of  is bounded below everywhere by anyone of its tangents.
is bounded below everywhere by anyone of its tangents.
Restriction to a line
The function  is convex if and only if its restriction to /any} line is convex, meaning that for every
is convex if and only if its restriction to /any} line is convex, meaning that for every 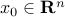 , and
, and 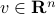 , the function
, the function 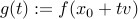 is convex.
is convex.
Examples:
Second-order condition
If  is twice differentiable, then it is convex if and only if its Hessian
is twice differentiable, then it is convex if and only if its Hessian 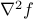 is positive semi-definite everywhere on the domain of
is positive semi-definite everywhere on the domain of  . This is perhaps the most commonly known characterization of convexity.
. This is perhaps the most commonly known characterization of convexity.
Examples:
Operations that preserve convexity
Composition with an affine function
The composition with an affine function preserves convexity: if 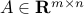 ,
, 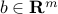 and
and 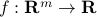 is convex, then the function
is convex, then the function 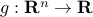 with values
with values 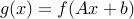 is convex.
is convex.
Point-wise maximum
The pointwise maximum of a family of convex functions is convex: if 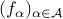 is a family of convex functions index by
is a family of convex functions index by 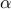 , then the function
, then the function
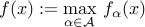
is convex. This is one of the most powerful ways to prove convexity.
Examples:
Dual norm: for a given norm, we define the dual norm as the function
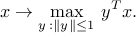
This function is convex, as the maximum of convex (in fact, linear) functions (indexed by the vector 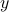 ). The dual norm earns its name, as it satisfies the properties of a norm.
). The dual norm earns its name, as it satisfies the properties of a norm.
Largest singular value of a matrix: Another example is the largest singular value (see also here) of a matrix
 :
:
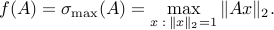
Here, each function (indexed by  )
) 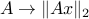 is convex, since it is the composition of the Euclidean norm (a convex function) with an affine function
is convex, since it is the composition of the Euclidean norm (a convex function) with an affine function 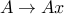 .
.
Nonnegative weighted sum
The nonnegative weighted sum of convex functions is convex.
Example: Negative entropy function.
Partial minimum
If  is a convex function in
is a convex function in 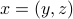 , then the function
, then the function  is convex. (Note that joint convexity in
is convex. (Note that joint convexity in 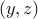 is essential.)
is essential.)
Example:
Case when
 is quadratic: the Schur complement lemma.
is quadratic: the Schur complement lemma.
Composition with monotone convex functions
The composition with another function does not always preserve convexity.
However, if 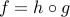 , with
, with 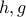 convex and
convex and 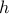 increasing, then
increasing, then  is convex.
is convex.
Indeed, the condition 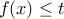 is equivalent to the existence of
is equivalent to the existence of 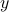 such that
such that
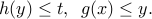
The condition above defines a convex set in the space of 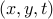 -variables. The epigraph of
-variables. The epigraph of  is thus the projection of that convex set on the space of
is thus the projection of that convex set on the space of 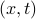 -variables, hence it is convex.
-variables, hence it is convex.
Example: proving convexity via monotonicity.
More generally, if the functions 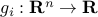 ,
, 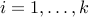 are convex and
are convex and 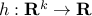 is convex and non-decreasing in each argument, with
is convex and non-decreasing in each argument, with  , then
, then 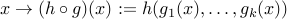 is convex.
is convex.
For example, if 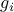 's are convex, then
's are convex, then 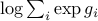 also is.
also is.