Convex Sets

Convex Optimization > Convex sets | Convex functions | Convex optimization problems | Algorithms | DCP

Definition
Operations that preserve convexity
Separation theorems
- Separating hyperplanes
- Supporting hyperplanes

Definitions

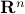A subset mathbf{C} of $mathbf{R}^n$ is said to be convex if and only if it contains the line segment between any two points in it:

$forall : x_1, x_2 in mathbf{C}, ;; forall : lambda in [0,1] ~:~ lambda x_1 + (1-lambda) x_2 in mathbf{C}.$

Subspaces and affine sets, such as lines, planes and higher-dimensional ‘‘flat’’ sets, are obviously convex, as they contain the entire line passing through any two points, not just the line segment. That is, there is no restriction on the scalar 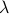lambda anymore in the above condition.

Examples:

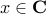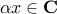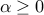A set is said to be a convex cone if it is convex, and has the property that if x in mathbf{C} , then alpha x in mathbf{C} for every alpha ge 0 .

Operations that preserve convexity

Intersection

The intersection of a (possibly infinite) family of convex sets is convex. This property can be used to prove convexity for a wide variety of situations.

Examples:

Affine transformation

If a map 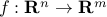$f :mathbf{R}^n rightarrow mathbf{R}^m$ is affine, and mathbf{C} is convex, then the set

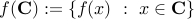
f(mathbf{C}) := left{ f(x) ~:~ x in mathbf{C} right}

is convex.

In particular, the projection of a convex set on a subspace is convex.

Example: Projection of a convex set on a subspace.

Separation theorems

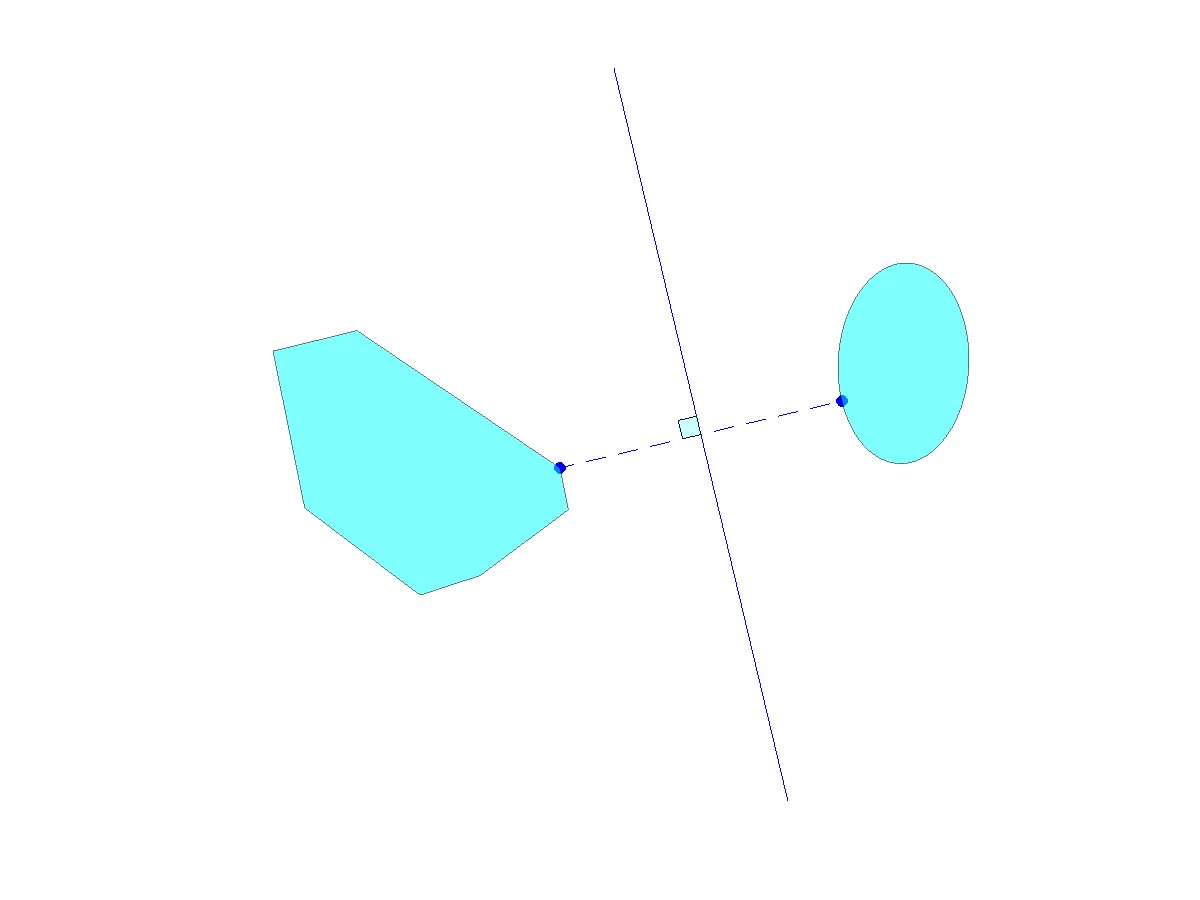
Separation theorems are one of the most important tools in convex optimization. They convex the intuitive idea that two convex sets that do not intersect can be separated by a straight line.

There are many versions of separation theorems. One of them is the separating hyperplane theorem:

Theorem: Separating hyperplane

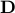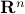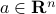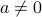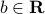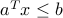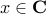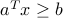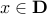If mathbf{C} , mathbf{D} are two convex subsets of $mathbf{R}^n$ that do not intersect, then there is an hyperplane that separates them, that is, there exit $a in mathbf{R}^n$ , a ne 0 , and b in mathbf{R} , such that a^Tx le b for every x in mathbf{C} , and a^Tx ge b for every x in mathbf{D} .

When two convex sets do not intersect, it is possible to find a hyperplane that separates them. In two dimensions, we can picture the hyperplane as a straight line. The proof of the separation theorem relies on finding the two points in each set that are closest to each other.

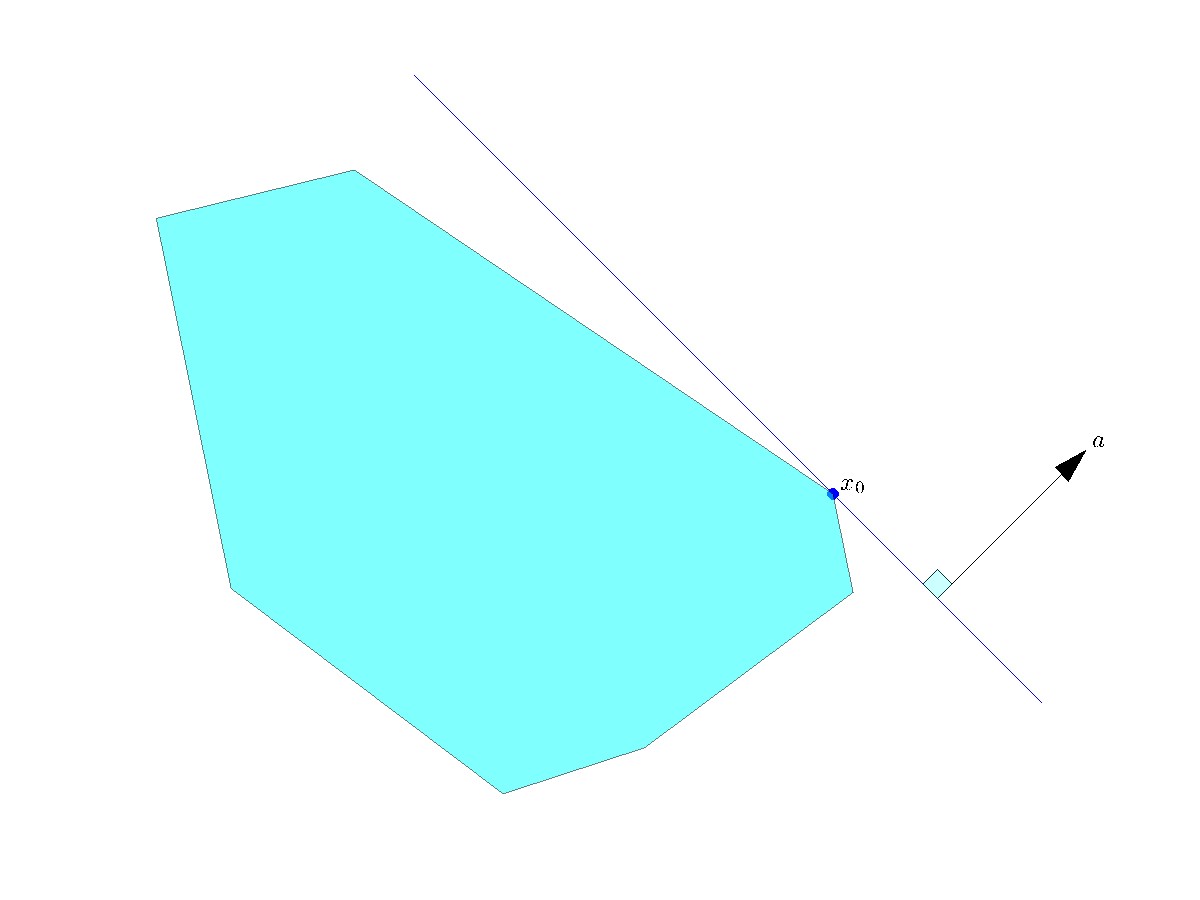
Another result involves the separation of a set from a point on its boundary:

Theorem: Supporting hyperplane

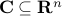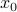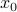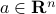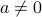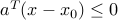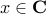If $mathbf{C} subseteq mathbf{R}^n$ is convex and non-empty, then for any x_0 at the boundary of , there exist a supporting hyperplane to at x_0 , meaning that there exist $a in mathbf{R}^n$ , a ne 0 , such that a^T(x-x_0) le 0 for every x in mathbf{C} .

It is always possible to separate (not strictly) a convex set from any point x_0 on its boundary. The separating hyperplane contains the point and the whole set lies on one side of the hyperplane. The supporting hyperplane may not be unique.