Convex Optimization Problems

Convex Optimization > Convex sets | Convex functions | Convex optimization problems | Algorithms | DCP

Definition
Optimality
Maximizing a convex function

Definition

The optimization problem in standard form:

$displaystylemin_x : f_0(x) ~:~ begin{array}[t]{l} f_i(x) le 0,quad i=1,cdots, m, h_i(x) = 0 quad i=1,cdots,p, end{array}$

is called a convex optimization problem if:

the objective function 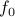is convex;
the functions defining the inequality constraints, 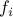, 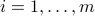are convex;
the functions defining the equality constraints, 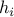, 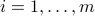are affine.

Note that, in the convex optimization model, we do not tolerate equality constraints, unless they are affine.

Optimality

Local and global optima

Recall the definition of global and local optima given here.

Theorem: Global vs. local optima in convex optimization

For convex problems, any locally optimal point is globally optimal. In addition, the optimal set is convex. (Proof)

Optimality condition

Consider the optimization problem above, which we write as

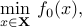
$min_{x in mathbf{X}} : f_0(x),$

where 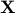mathbf{X} is the feasible set.

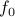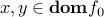When f_0 is differentiable, then we know that for every $x,y in {bf dom} f_0$ ,

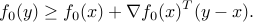
f_0(y) ge f_0(x) + nabla f_0(x) ^T (y-x).

Then is optimal if and only if

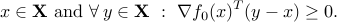
$x in mathbf{X} mbox{ and } forall : y in mathbf{X} ~:~ nabla f_0(x) ^T (y-x) ge 0 .$

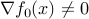If nabla f_0(x) ne 0 , then it defines a supporting hyperplane to the feasible set at .

When the problem is unconstrained, we obtain the optimality condition:

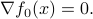
Note that these conditions are not always feasible, since the problem may not have any minimizer. This can happen for example when the optimal value is only attained in the limit; or, in constrained problems, when the feasible set is empty.

Examples:

The optimality conditions given above might be hard to solve. We will return to this issue later.

Maximization of convex functions

Sometimes we would like to maximize a convex function over a set 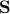mathbf{S} . Such problems are usually hard to solve.

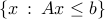For example, the problem of maximizing the distance from a given point (say, ) to a point in a polyhedron described as { x ::: Ax le b} is an example of such hard problems.

One important property of convex functions is that their maximum over any set is the same as the maximum over the convex hull of that set. That is, for any set 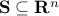$mathbf{S} subseteq mathbf{R}^n$ and any convex function 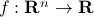$f : mathbf{R}^n rightarrow mathbf{R}$ , we have

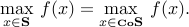
$max_{x in mathbf{S}} : f(x) = max_{x in mbox{tinybf Co}mathbf{S}} : f(x).$

In the example mentioned above, where we seek to maximize the Euclidean norm of a point in a polyhedron, if we know the vertices of the polyhedron, that is, we can express the polyhedron as

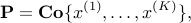
$mathbf{P} = mbox{bf Co}{ x^{(1)},ldots,x^{(K)}},$

then the optimal distance is simply 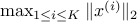$max_{1 le i le K}|x^{(i)}|_2$ .

Unfortunately, in practice, finding the vertices (given the original representation of 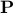mathbf{P} as an intersection of hyperplanes) is hard, as the polytope might have an exponential number of vertices.