Algorithms for Convex Optimization
From Least-Squares to convex minimization
Unconstrained minimization via Newton's method
Interior-point methods
Gradient methods
From Least-Squares to convex minimization
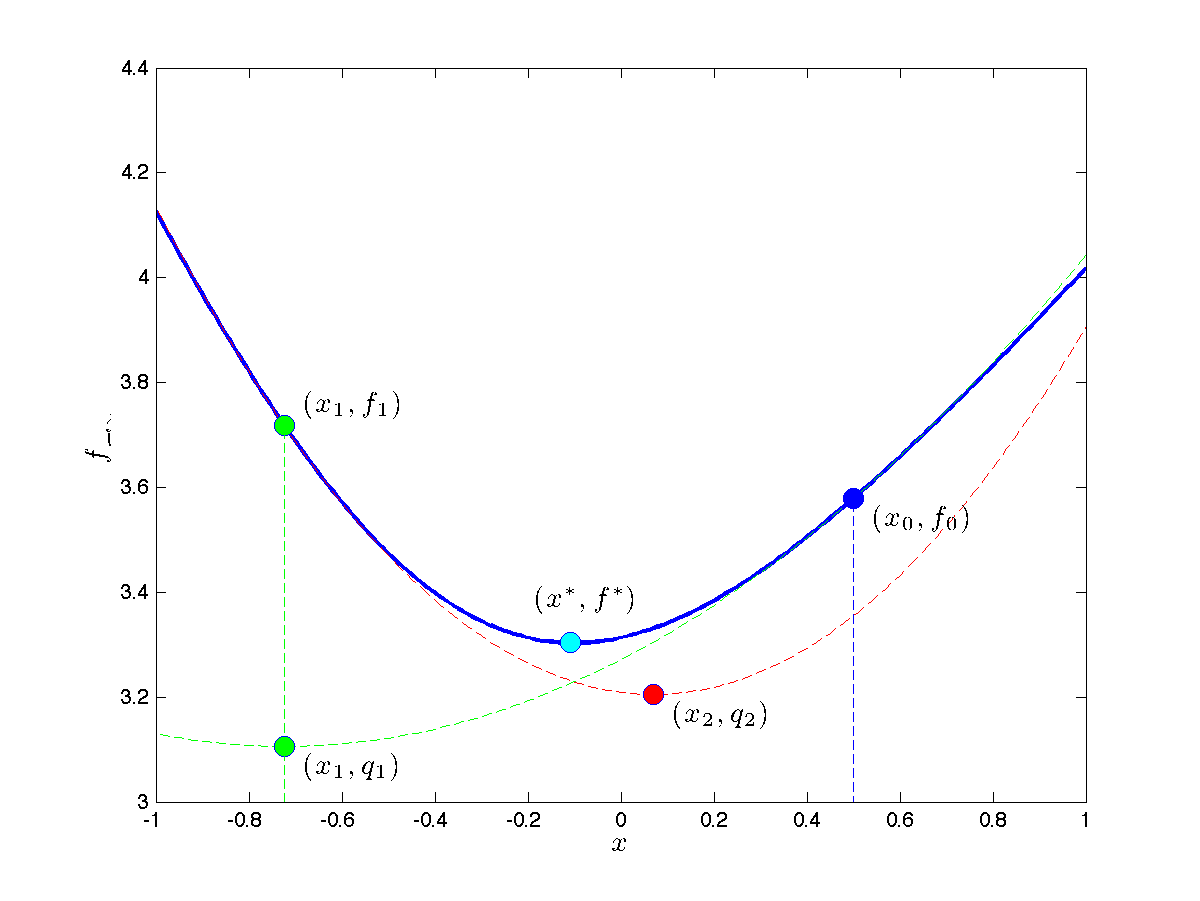
We have seen how ordinary least-squares (OLS) problems can be solved using linear algebra (e.g. SVD) methods. Using OLS, we can minimize convex, quadratic functions of the form
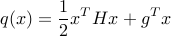
when 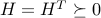 . This last requirement ensures that the function
. This last requirement ensures that the function  is convex. For such convex quadratic functions, as for any convex functions, any local minimum is global. In fact, when
is convex. For such convex quadratic functions, as for any convex functions, any local minimum is global. In fact, when 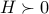 , then the unique minimizer is
, then the unique minimizer is 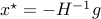 .
.
It turns out one can leverage the approach to minimizing more general functions, using an iterative algorithm, based on a local quadratic approximation of the the function at the current point. The approach can then be extended to problems with constraints, by replacing the original constrained problem with an unconstrained one, in which the constraints are penalized in the objective.
Unconstrained minimization: Newton's method
We consider an unconstrained minimization problem, where we seek to minimize a function twice-differentiable function  . Let us assume that the function under consideration is strictly convex, which is to say that its Hessian is positive definite everywhere. (If
. Let us assume that the function under consideration is strictly convex, which is to say that its Hessian is positive definite everywhere. (If  is not convex, we might run into a local minima.)
is not convex, we might run into a local minima.)
For minimizing convex functions, an iterative procedure could be based on a simple quadratic approximation procedure known as Newton's method. We start with initial guess 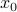 . At each step
. At each step 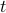 , we update our current guess
, we update our current guess 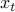 by minimizing the second-order approximation
by minimizing the second-order approximation 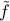 of
of  at
at 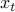 , which is the quadratic function (see here)
, which is the quadratic function (see here)
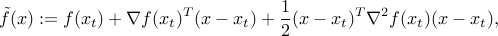
where 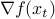 denotes the gradient, and
denotes the gradient, and 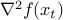 the Hessian, of
the Hessian, of  at
at 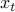 . Our next guess
. Our next guess 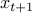 , will be set to be a solution to the problem of minimizing
, will be set to be a solution to the problem of minimizing 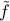 . Since the function is strictly convex, we have
. Since the function is strictly convex, we have 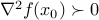 , so that the problem we are solving at each step has a unique solution, which corresponds to the global minimum of
, so that the problem we are solving at each step has a unique solution, which corresponds to the global minimum of 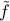 .
The basic Newton iteration is thus
.
The basic Newton iteration is thus
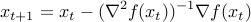
This idea will fail for general (non-convex) functions. It might even fail for some convex functions. However, for a large class of convex functions, knwon as self-concordant functions, a variation on the Newton method works extremely well, and is guaranteed to find the global minimizer of the function  . For such functions, the Hessian does not vary too fast, which turns out to be a crucial ingredient for the success of Newton's method.
. For such functions, the Hessian does not vary too fast, which turns out to be a crucial ingredient for the success of Newton's method.
Constrained minimization: interior-point methods
The method above can be applied to the more general context of convex optimization problems of standard form:
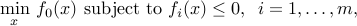
where every function involved is twice-differentiable, and convex.
The basic idea behind interior-point methods is to replace the constrained problem by an unconstrained one, involving a function that is constructed with the original problem functions. One further idea is to use a logarithmic barrier: in lieu of the original problem, we address
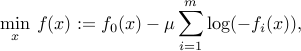
where 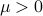 is a small parameter. The function
is a small parameter. The function  turns out to be convex, as long as
turns out to be convex, as long as 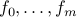 are.
are.
For 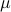 large, solving the above problem results in a point well ‘‘inside’’ the feasible set, an ‘‘interior point’’. As
large, solving the above problem results in a point well ‘‘inside’’ the feasible set, an ‘‘interior point’’. As 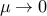 the solution converges to a global minimizer for the original, constrained problem. In fact, the theory of convex optimization says that if we set
the solution converges to a global minimizer for the original, constrained problem. In fact, the theory of convex optimization says that if we set 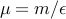 , then a minimizer to the above function is
, then a minimizer to the above function is  -suboptimal. In practice, algorithms do not set the value of
-suboptimal. In practice, algorithms do not set the value of 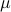 so aggressively, and update the value of
so aggressively, and update the value of 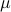 a few times.
a few times.
For a large class of convex optimization problems, the function  is self-concordant, so that we can safely apply Newton's method to the minimization of the above function. In fact, for a large class of convex optimization problems, the method converges in time polynomial in
is self-concordant, so that we can safely apply Newton's method to the minimization of the above function. In fact, for a large class of convex optimization problems, the method converges in time polynomial in 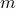 .
.
The interior-point approach is limited by the need to form the gradient and Hessian of the function  above. For extremely large-scale problems, this task may be too daunting.
above. For extremely large-scale problems, this task may be too daunting.
Gradient methods
Unconstrained case
Gradient methods offer an alternative to interior-point methods, which is attractive for large-scale problems. Typically, these algorithms need a considerably larger number of iterations compared to interior-point methods, but each iteration is much cheaper to process.
Perhaps the simplest algorithm to minimizing a convex function involves the iteration
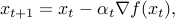
where 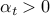 is a parameter. The interpretation of the algorithm is that it tries to decrease the value of the function by taking a step in the direction of the negative gradient. For small enough value of
is a parameter. The interpretation of the algorithm is that it tries to decrease the value of the function by taking a step in the direction of the negative gradient. For small enough value of 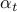 , indeed we have
, indeed we have 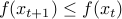 .
.
Depending on the choice of the parameter 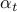 (as as function of the iteration number
(as as function of the iteration number 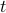 ), and some properties on the function
), and some properties on the function  , convergence can be rigorously proven.
, convergence can be rigorously proven.
Constrained case
The gradient method can be adapted to constrained problems, via the iteration
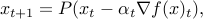
where 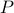 is the projection operator, which to its argument
is the projection operator, which to its argument  associates the point closest (in Euclidean norm sense) to
associates the point closest (in Euclidean norm sense) to  in
in  . Depending on problem structure, this projection may or may not be easy to perform.
. Depending on problem structure, this projection may or may not be easy to perform.
Example: Box-constrained least-squares.
 with domain the whole
with domain the whole 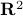 , and values
, and values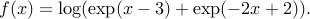
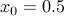 is formed (dotted line in green). The corresponding minimizer is the new iterate,
is formed (dotted line in green). The corresponding minimizer is the new iterate, 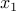 . The Newton algorithm proceeds to form a new quadratic approximation of the function at that point (dotted line in red), leading to the second iterate,
. The Newton algorithm proceeds to form a new quadratic approximation of the function at that point (dotted line in red), leading to the second iterate, 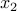 . Although
. Although 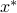 (in light blue),
(in light blue), 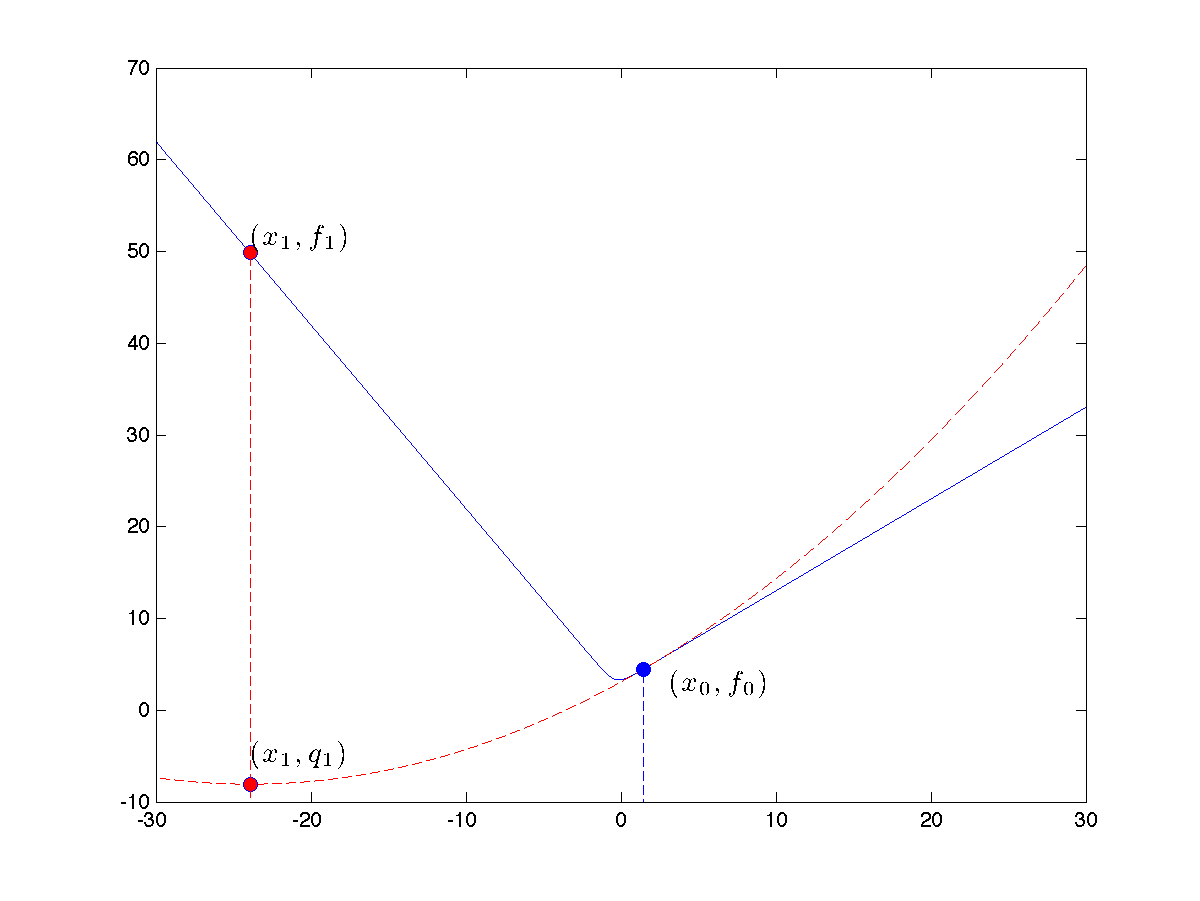
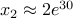 .
.