Definitions
Symmetric matrices and quadratic functions
Second-order approximation of non-linear functions
Special symmetric matrices
Symmetric matrices and quadratic functions
Symmetric matrices
A square matrix 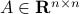 is symmetric if it is equal to its transpose. That is,
is symmetric if it is equal to its transpose. That is,
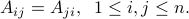
The set of symmetric 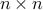 matrices is denoted
matrices is denoted 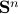 . This set is a subspace of
. This set is a subspace of 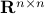 .
.
Examples:
Gram matrix of data points.
Quadratic functions
A function 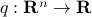 is said to be a quadratic function if it can be expressed as
is said to be a quadratic function if it can be expressed as
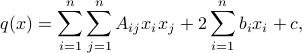
for numbers 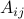 ,
, 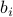 , and
, and  ,
, 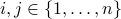 . A quadratic function is thus an affine combination of the
. A quadratic function is thus an affine combination of the 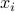 's and all the ‘‘cross-products’’
's and all the ‘‘cross-products’’ 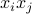 . We observe that the coefficient of
. We observe that the coefficient of 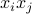 is
is 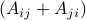 .
.
The function is said to be a quadratic form if there are no linear or constant terms in it: 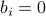 ,
,  .
.
Note that the Hessian (matrix of second-derivatives) of a quadratic function is constant.
Examples:
Link between quadratic functions and symmetric matrices
There is a natural relationship between symmetric matrices and quadratic functions. Indeed, any quadratic function 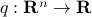 can be written as
can be written as
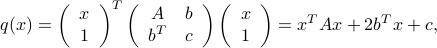
for an appropriate symmetric matrix 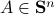 , vector
, vector 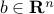 and scalar
and scalar 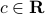 . Here,
. Here, 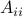 is the coefficient of
is the coefficient of 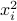 in
in 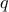 ; for
; for 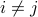 ,
, 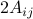 is the coefficient of the term
is the coefficient of the term 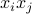 in
in 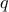 ;
; 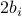 is that of
is that of 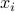 ; and
; and  is the constant term,
is the constant term, 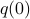 . If
. If 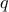 is a quadratic form, then
is a quadratic form, then  ,
,  , and we can write
, and we can write 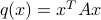 where now
where now  .
.
Examples:
Second-order approximations of non-quadratic functions
We have seen here how linear functions arise when one seeks a simple, linear approximation to a more complicated non-linear function. Likewise, quadratic functions arise naturally when one seeks to approximate a given non-quadratic function by a quadratic one.
One-dimensional case
If 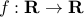 is a twice-differentiable function of a single variable, then the second order approximation (or, second-order Taylor expansion) of
is a twice-differentiable function of a single variable, then the second order approximation (or, second-order Taylor expansion) of  at a point
at a point 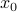 is of the form
is of the form
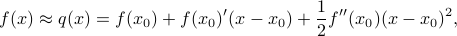
where 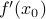 is the first derivative, and
is the first derivative, and 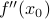 the second derivative, of
the second derivative, of  at
at 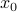 . We observe that the quadratic approximation
. We observe that the quadratic approximation 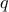 has the same value, derivative, and second-derivative as
has the same value, derivative, and second-derivative as  , at
, at 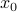 .
.
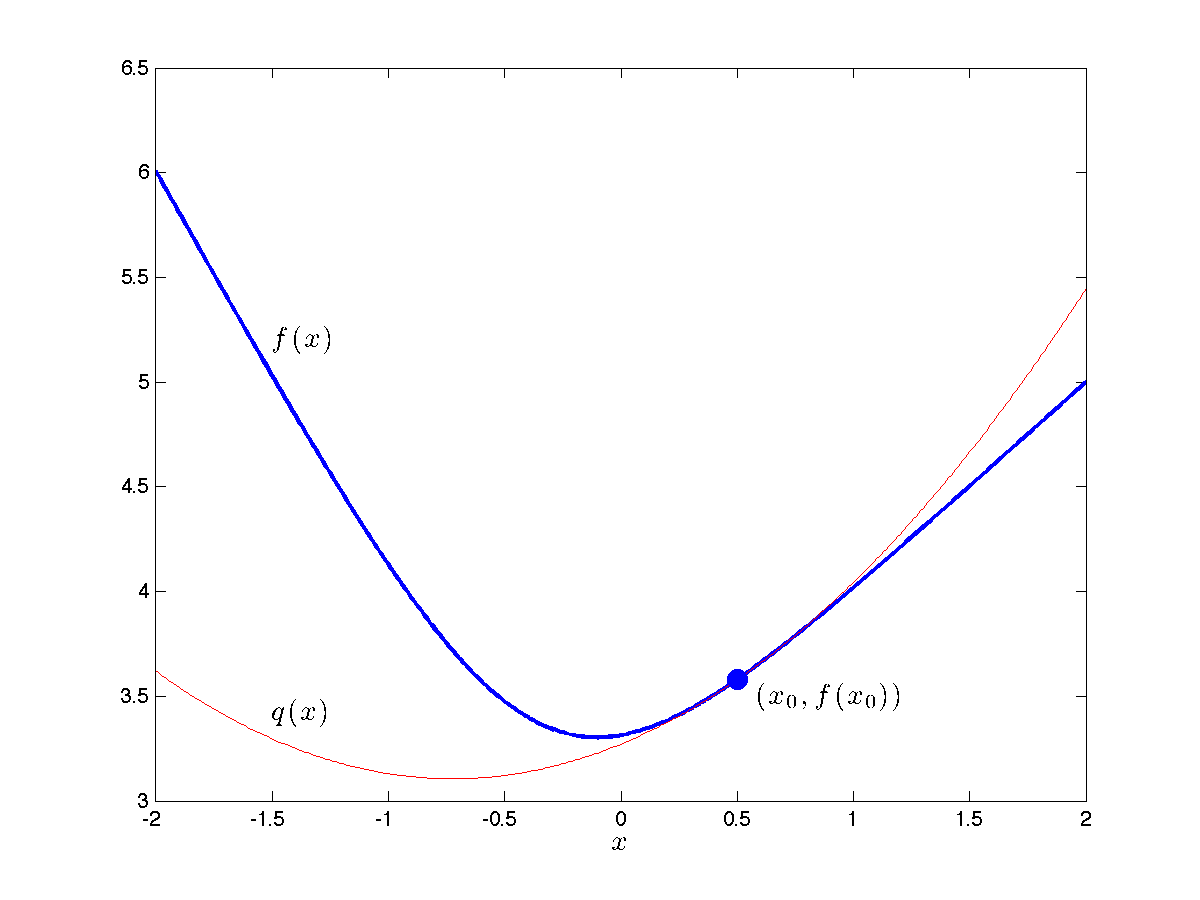 |
Example: The figure shows a second-order approximation 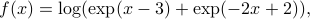
at the point |
Multi-dimensional case
In multiple dimensions, we have a similar result. Let us approximate a twice-differentiable function 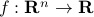 by a quadratic function
by a quadratic function 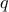 , so that
, so that  and
and 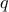 coincide up and including to the second derivatives.
coincide up and including to the second derivatives.
The function 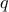 must be of the form
must be of the form
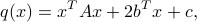
where  ,
, 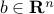 , and
, and 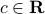 . Our condition that
. Our condition that 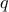 coincides with
coincides with  up and including to the second derivatives shows that we must have
up and including to the second derivatives shows that we must have
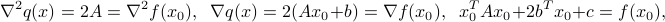
where 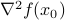 is the Hessian, and
is the Hessian, and 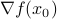 the gradient, of
the gradient, of  at
at 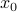 .
.
Solving for 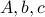 we obtain the following result:
we obtain the following result:
Second-order expansion of a function.
The second-order approximation ofa twice-differentiable function  at a point
at a point 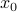 is of the form
is of the form
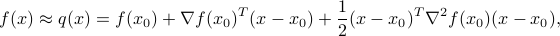
where 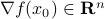 is the gradient of
is the gradient of  at
at 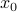 , and the symmetric matrix
, and the symmetric matrix 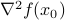 is the Hessian of
is the Hessian of  at
at 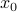 .
. 
Example: Second-order expansion of the log-sum-exp function.
Special symmetric matrices
Diagonal matrices
Perhaps the simplest special case of symmetric matrices is the class of diagonal matrices, which are non-zero only on their diagonal.
If 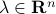 , we denote by
, we denote by 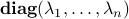 , or
, or 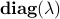 for short, the
for short, the 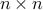 (symmetric) diagonal matrix with
(symmetric) diagonal matrix with 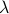 on its diagonal. Diagonal matrices correspond to quadratic functions of the form
on its diagonal. Diagonal matrices correspond to quadratic functions of the form
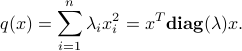
Such functions do not have any ‘‘cross-terms’’ of the form 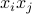 with
with 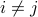 .
.
Example: A diagonal matrix and its associated quadratic form.
Symmetric dyads
Another important class of symmetric matrices is that of the form 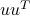 , where
, where 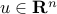 . The matrix has elements
. The matrix has elements 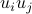 , and is symmetric. Such matrices are called symmetric dyads. (If
, and is symmetric. Such matrices are called symmetric dyads. (If 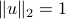 , then the dyad is said to be normalized.)
, then the dyad is said to be normalized.)
Symmetric dyads corresponds to quadratic functions that are simply squared linear forms: 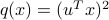 .
.
Example: A squared linear form.
 example
example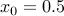 (in red).
(in red).