Gram matrix
Consider 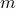
 -vectors
-vectors 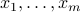 . The Gram matrix of the collection is the
. The Gram matrix of the collection is the 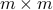 matrix
matrix 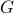 with elements
with elements 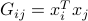 . The matrix can be expressed compactly in terms of the matrix
. The matrix can be expressed compactly in terms of the matrix ![X = [x_1,ldots,x_m]](eqs/6993711612918051957-130.png) , as
, as
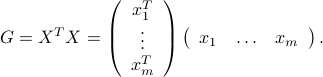
By construction, a Gram matrix is always symmetric, meaning that 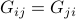 for every pair
for every pair 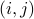 . It is also positive semi-definite, meaning that
. It is also positive semi-definite, meaning that 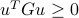 for every vector
for every vector 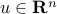 (this comes from the identity
(this comes from the identity 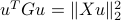 ).
).
Assume that each vector 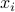 is normalized:
is normalized: 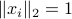 . Then the coefficient
. Then the coefficient 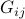 can be expressed as
can be expressed as
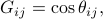
where 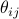 is the angle between the vectors
is the angle between the vectors 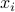 and
and 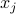 . Thus
. Thus 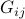 is a measure of how similar
is a measure of how similar 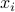 and
and 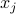 are.
are.
The matrix 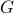 arises for example in text document classification, with
arises for example in text document classification, with 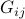 a measure of similarity between the
a measure of similarity between the 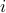 -th and
-th and 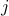 -th document, and
-th document, and 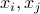 their respective bag-of-words representation (normalized to have Euclidean norm
their respective bag-of-words representation (normalized to have Euclidean norm  ).
).
See also: