Positive Semi-Definite Matrices
Definitions
Special cases and examples
Square root and Cholesky decomposition
Ellipsoids
Definitions
For a given symmetric matrix 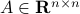 , the associated quadratic form is the function
, the associated quadratic form is the function 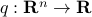 with values
with values
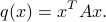
A symmetric matrix
 is said to be positive semi-definite (PSD, notation:
is said to be positive semi-definite (PSD, notation: 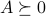 ) if and only if the associated quadratic form
) if and only if the associated quadratic form 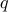 is non-negative everywhere:
is non-negative everywhere:
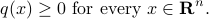
It is said to be positive definite (PD, notation:
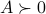 ) if the quadratic form is non-negative, and definite, that is,
) if the quadratic form is non-negative, and definite, that is, 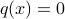 if and only if
if and only if 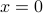 .
.
It turns out that a matrix is PSD if and only if the eigenvalues of  are non-negative. Thus, we can check if a form is PSD by computing the eigenvalue decomposition of the underlying symmetric matrix.
are non-negative. Thus, we can check if a form is PSD by computing the eigenvalue decomposition of the underlying symmetric matrix.
A quadratic form 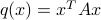 , with
, with  is non-negative (resp. positive-definite) if and only if every eigenvalue of the symmetric matrix
is non-negative (resp. positive-definite) if and only if every eigenvalue of the symmetric matrix  is non-negative (resp. positive).
is non-negative (resp. positive).
By definition, the PSD and PD properties are properties of the eigenvalues of the matrix only, not of the eigenvectors. Also, if the 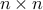 matrix
matrix  is PSD, then for every matrix
is PSD, then for every matrix 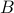 with
with  columns, the matrix
columns, the matrix 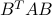 also is.
also is.
Special cases and examples
Symmetric dyads
Special cases of PSD matrices include symmetric dyads. Indeed, if 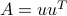 for some vector
for some vector 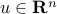 , then for every
, then for every  :
:
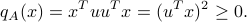
More generally if 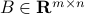 , then
, then 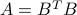 is PSD, since
is PSD, since
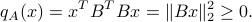
Diagonal matrices
A diagonal matrix is PSD (resp. PD) if and only if all of its (diagonal) elements are non-negative (resp. positive).
Examples of PSD matrices
Gram matrix of data points.
Square root and Cholesky decomposition
For PD matrices, we can generalize the notion of ordinary square root of a non-negative number. Indeed, if  is PSD, there exist a unique PSD matrix, denoted
is PSD, there exist a unique PSD matrix, denoted 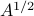 , such that
, such that 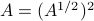 . We can express this matrix square root in terms of the SED of
. We can express this matrix square root in terms of the SED of 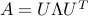 , as
, as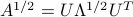 , where
, where 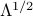 is obtained from
is obtained from 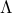 by taking the square root of its diagonal elements. If
by taking the square root of its diagonal elements. If  is PD, then so is its square root.
is PD, then so is its square root.
Any PSD matrix can be written as a product 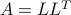 for an appropriate matrix
for an appropriate matrix 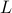 . The decomposition is not unique, and
. The decomposition is not unique, and 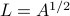 is only a possible choice (the only PSD one). Another choice, in terms of the SED of
is only a possible choice (the only PSD one). Another choice, in terms of the SED of 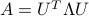 , is
, is 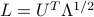 . If
. If  is positive-definite, then we can choose
is positive-definite, then we can choose 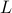 to be lower triangular, and invertible. The decomposition is then known as the Cholesky decomposition of
to be lower triangular, and invertible. The decomposition is then known as the Cholesky decomposition of  .
.
Ellipsoids
There is a strong correspondence between ellipsoids and PSD matrices.
Definition
We define an ellipsoid to be affine transformation of the unit ball for the Euclidean norm:
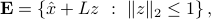
where 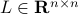 is an arbitrary non-singular matrix. We can express the ellipsoid as
is an arbitrary non-singular matrix. We can express the ellipsoid as
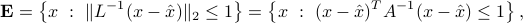
where 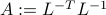 is PD.
is PD.
Geometric interpretation via SED
We can interpret the eigenvectors and associated eigenvalues of  in terms of geometrical properties of the ellipsoid, as follows. Consider the SED of
in terms of geometrical properties of the ellipsoid, as follows. Consider the SED of  :
: 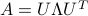 , with
, with 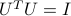 and
and 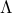 diagonal, with diagonal elements positive. The SED of its inverse is
diagonal, with diagonal elements positive. The SED of its inverse is 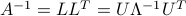 . Let
. Let 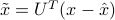 . We can express the condition
. We can express the condition 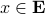 as
as
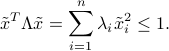
Now set 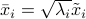 ,
, 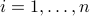 . The above writes
. The above writes 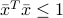 : in
: in 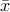 -space, the ellipsoid is simply an unit ball. In
-space, the ellipsoid is simply an unit ball. In 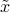 -space, the ellipsoid corresponds to scaling each
-space, the ellipsoid corresponds to scaling each 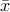 -axis by the square roots of the eigenvalues. The ellipsoid has principal axes parallel to the coordinate axes in
-axis by the square roots of the eigenvalues. The ellipsoid has principal axes parallel to the coordinate axes in 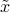 -space. We then apply a rotation and a translation, to get the ellipsoid in the original
-space. We then apply a rotation and a translation, to get the ellipsoid in the original  -space. The rotation is determined by the eigenvectors of
-space. The rotation is determined by the eigenvectors of 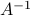 , which are contained in the orthogonal matrix
, which are contained in the orthogonal matrix 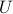 . Thus, the geometry of the ellipsoid can be read from the SED of the PD matrix
. Thus, the geometry of the ellipsoid can be read from the SED of the PD matrix 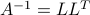 : the eigenvectors give the principal directions, and the semi-axis lengths are the square root of the eigenvalues.
: the eigenvectors give the principal directions, and the semi-axis lengths are the square root of the eigenvalues.
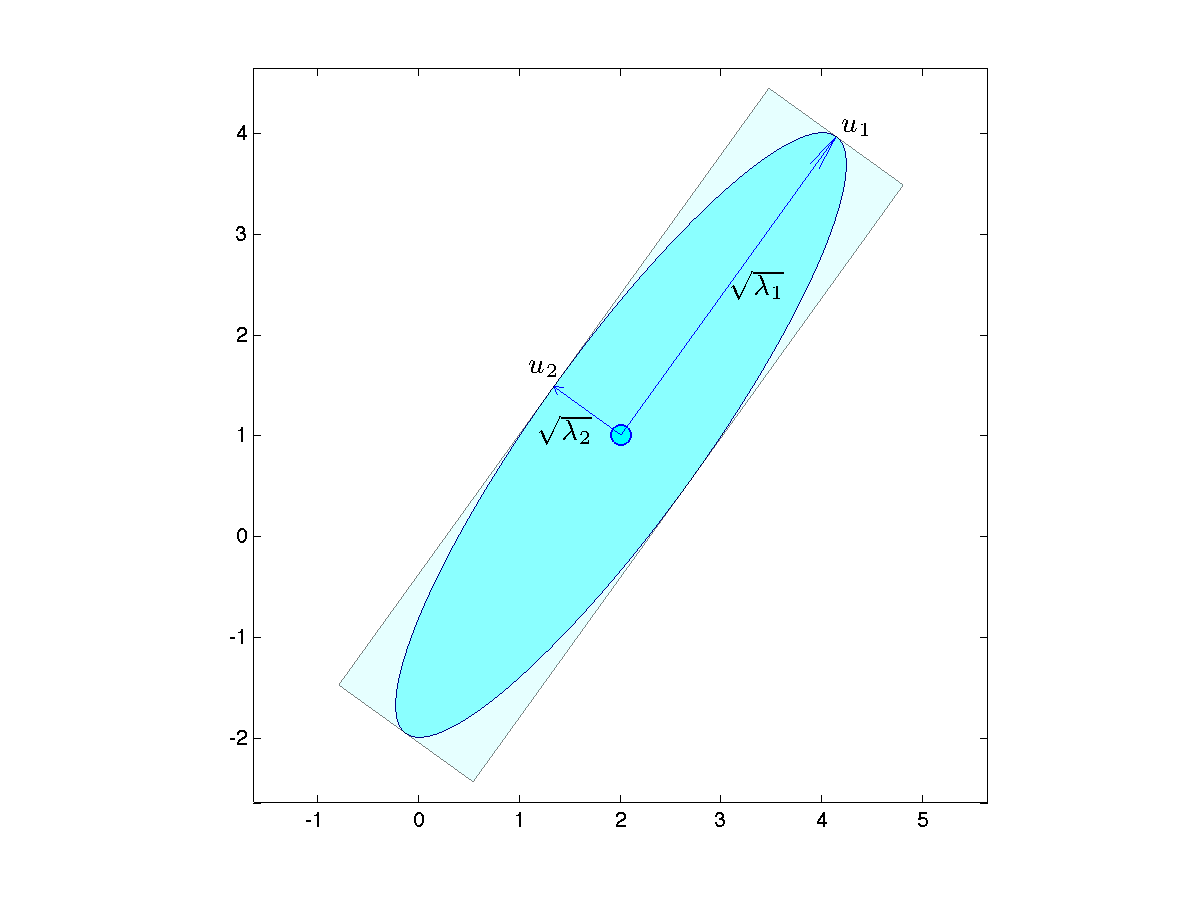 |
The graph on the left shows the ellipsoid 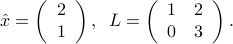
The matrix 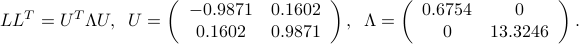
We check that the columns of |
The above shows in particular that an equivalent representation of an ellipsoid is
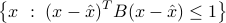
where 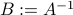 is PD.
is PD.
It is possible to define degenerate ellipsoids, which correspond to cases when the matrix 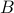 in the above, or its inverse
in the above, or its inverse  , is degenerate. For example, cylinders or slabs (intersection of two parallel half-spaces) are degenerate ellipsoids.
, is degenerate. For example, cylinders or slabs (intersection of two parallel half-spaces) are degenerate ellipsoids.
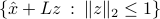 , with
, with 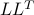 admits the SED
admits the SED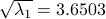 ,
, 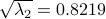 are the semi-axis lengths.
are the semi-axis lengths.