The SVD theorem
The SVD theorem
Geometry
Link with the spectral theorem
The SVD theorem
Basic idea
Recall from here that any matrix 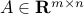 with rank one can be written as
with rank one can be written as
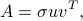
where 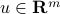 ,
, 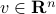 , and
, and 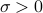 .
.
It turns out that a similar result holds for matrices of arbitrary rank  . That is, we can express any matrix
. That is, we can express any matrix 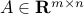 with rank one as sum of rank-one matrices
with rank one as sum of rank-one matrices
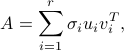
where 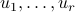 are mutually orthogonal,
are mutually orthogonal, 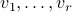 are also mutually orthogonal, and the
are also mutually orthogonal, and the 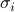 's are positive numbers called the singular values of
's are positive numbers called the singular values of  . In the above,
. In the above,  turns out to be the rank of
turns out to be the rank of  .
.
Theorem statement
The following important result applies to any matrix  , and allows to understand the structure of the mapping
, and allows to understand the structure of the mapping 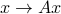 .
.
An arbitrary matrix 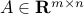 admits a decomposition of the form
admits a decomposition of the form
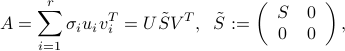
where 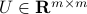 ,
, 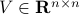 are both orthogonal matrices, and the matrix
are both orthogonal matrices, and the matrix 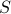 is diagonal:
is diagonal:
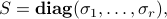
where the positive numbers 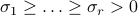 are unique, and are called the singular values of
are unique, and are called the singular values of  . The number
. The number 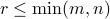 is equal to the rank of
is equal to the rank of  , and the triplet
, and the triplet 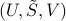 is called a singular value decomposition (SVD) of
is called a singular value decomposition (SVD) of  . The first
. The first  columns of
columns of 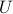 :
: 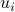 ,
, 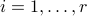 (resp.
(resp. 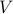 :
: 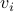 ,
, 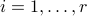 ) are called left (resp. right) singular vectors of
) are called left (resp. right) singular vectors of  , and satisfy
, and satisfy
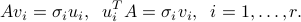
The proof of the theorem hinges on the spectral theorem for symmetric matrices. Note that in the theorem, the zeros appearing alongside 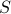 are really blocks of zeros. They may be empty, for example if
are really blocks of zeros. They may be empty, for example if 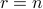 , then there are no zeros to the right of
, then there are no zeros to the right of 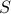 .
.
Computing the SVD
The SVD of a 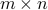 matrix
matrix  can be easily computed via a sequence of linear transformations. The complexity of the algorithm, expressed roughly as the number of floating point operations per seconds it requires, grows as
can be easily computed via a sequence of linear transformations. The complexity of the algorithm, expressed roughly as the number of floating point operations per seconds it requires, grows as  . This can be substantial for large, dense matrices. For sparse matrices, we can speed up the computation if we are interested only in the largest few singular values and associated singular vectors.
. This can be substantial for large, dense matrices. For sparse matrices, we can speed up the computation if we are interested only in the largest few singular values and associated singular vectors.
>> [U,Stilde,V] = svd(A); % this produces the SVD of A, with Stilde of same size as A >> [Uk,Sk,Vk] = svds(A,k); % the k largest singular values of A, assuming A is sparse
Example: A 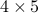 example.
example.
Geometry
The theorem allows to decompose the action of  on a given input vector as a three-step process. To get
on a given input vector as a three-step process. To get 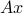 , where
, where  , we first form
, we first form 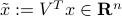 . Since
. Since 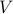 is an orthogonal matrix,
is an orthogonal matrix, 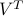 is also orthogonal, and
is also orthogonal, and 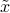 is just a rotated version of
is just a rotated version of  , which still lies in the input space. Then we act on the rotated vector
, which still lies in the input space. Then we act on the rotated vector 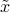 by scaling its elements. Precisely, the first
by scaling its elements. Precisely, the first  elements of
elements of 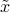 are scaled by the singular values
are scaled by the singular values 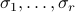 ; the remaining
; the remaining  elements are set to zero. This step results in a new vector
elements are set to zero. This step results in a new vector 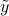 which now belongs to the output space
which now belongs to the output space 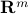 . The final step consists in rotating the vector
. The final step consists in rotating the vector 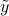 by the orthogonal matrix
by the orthogonal matrix 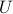 , which results in
, which results in 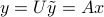 .
.
Example: Assume  has the simple form
has the simple form
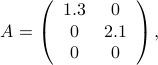
then for an input vector  in
in 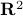 ,
, 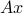 is a vector in
is a vector in 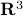 with first component
with first component 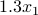 , second component
, second component 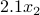 , and last component zero.
, and last component zero.
To summarize, the SVD theorem states that any matrix-vector multiplication can be decomposed as a sequence of three elementary transformations: a rotation in the input space, a scaling that goes from the input space to the output space, and a rotation in the output space. In contrast with symmetric matrices, input and output directions are different.
The interpretation allows to make a few statements about the matrix.
Example: A  example.
example.
Link with the SED
If  admits an SVD, then the matrices
admits an SVD, then the matrices 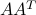 and
and 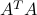 has the following SEDs:
has the following SEDs:
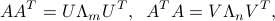
where 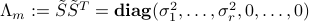 is
is 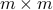 (so it has
(so it has 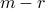 trailing zeros), and
trailing zeros), and 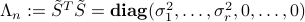 is
is 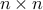 (so it has
(so it has  trailing zeros). The eigenvalues of
trailing zeros). The eigenvalues of 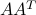 and
and 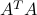 are the same, and equal to the squared singular values of
are the same, and equal to the squared singular values of  . The corresponding eigenvectors are the left and right singular vectors of
. The corresponding eigenvectors are the left and right singular vectors of  .
.
This is a method (not the most computationally efficient) to find the SVD of a matrix, based on the SED.