Singular value decomposition (SVD) theorem
An arbitrary matrix 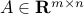 admits a decomposition of the form
admits a decomposition of the form
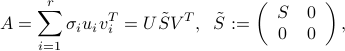
where 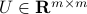 ,
, 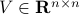 are both orthogonal matrices, and the matrix
are both orthogonal matrices, and the matrix 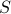 is diagonal:
is diagonal:
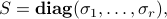
where the positive numbers 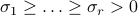 are unique, and are called the singular values of
are unique, and are called the singular values of  . The number
. The number 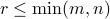 is equal to the rank of
is equal to the rank of  , and the triplet
, and the triplet 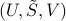 is called a singular value decomposition (SVD) of
is called a singular value decomposition (SVD) of  . The first
. The first  columns of
columns of 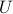 :
: 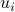 ,
, 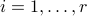 (resp.
(resp. 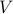 :
: 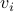 ,
, 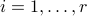 ) are called left (resp. right) singular vectors of
) are called left (resp. right) singular vectors of  , and satisfy
, and satisfy
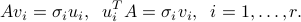
Proof: The matrix 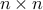
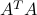 is real and symmetric. According to the spectral theorem, it admits an eigenvalue decomposition in the form
is real and symmetric. According to the spectral theorem, it admits an eigenvalue decomposition in the form  , with
, with 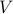 a
a 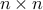 matrix whose columns form an orthonormal basis (that is,
matrix whose columns form an orthonormal basis (that is,  ), and
), and  . Here,
. Here,  is the rank of
is the rank of 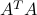 (if
(if 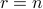 then there are no trailing zeros in
then there are no trailing zeros in 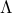 ). Since
). Since 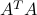 is positive semi-definite, the
is positive semi-definite, the  's are non-negative, and we can define the non-zero quantities
's are non-negative, and we can define the non-zero quantities  ,
,  .
.
Note that when  ,
,  , since then
, since then  .
.
Let us construct an 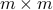 orthogonal matrix
orthogonal matrix 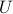 as follows. We set
as follows. We set

These 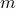 -vectors are unit-norm, and mutually orthogonal, since
-vectors are unit-norm, and mutually orthogonal, since  's are eigenvectors of
's are eigenvectors of 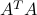 . Using (say) the Gram-Schmidt orthogonalization procedure, we can complete (if necessary, that is in the case
. Using (say) the Gram-Schmidt orthogonalization procedure, we can complete (if necessary, that is in the case  ) this set of vectors by
) this set of vectors by  in order to form an orthogonal matrix
in order to form an orthogonal matrix  .
.
Let us check that 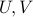 satisfy the conditions of the theorem, by showing that
satisfy the conditions of the theorem, by showing that  . We have
. We have

where the second line stems from the fact that  when
when  . Thus,
. Thus,  , as claimed.
, as claimed.