Optimization Models
Home
Software
Links
Index
Contact
1. Introduction
1.1. Overview
1.2. Optimization Models
2. Linear Algebra
2.1. Vectors
2.2. Matrices
2.3. Linear Equations
2.4.  Least-Squares
2.5. Eigenvalues
2.6  Singular Values
3. Convex Models
3.1. Convexity
3.2. LP and QP
3.3. SOCP
3.4. Robust LP
3.5. GP
3.6. SDP
3.7. Non-Convex Models
4. Duality
4.1. Weak Duality
4.2. Strong Duality
4.3.  Applications
5. Case Studies
5.1. Senate Voting
5.2. Antenna Arrays
5.3. Localization
5.4. Circuit Design

Solving Linear Equations via SVD

  • Solution set of a linear equation

  • Pseudo-inverse

  • Sensitivity analysis and condition number

Solution set

Consider a linear equation

Ax = y,

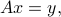
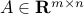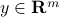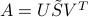where A in mathbf{R}^{m times n} and y in mathbf{R}^m are given. We can completely describe the set of solutions via SVD, as follows. Let us assume that A admits an SVD given here. With A = Utilde{ {S}}V^T, pre-multiply the linear equation by the inverse of 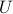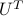U, U^T; then we express the equation in terms of the rotated vector 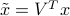tilde{x} = V^Tx. This leads to

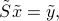
tilde{ {S}} tilde{x} = tilde{y},

where 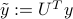tilde{y} := U^Ty is the ‘‘rotated’’ right-hand side of the equation. Due to the simple form of 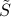tilde{ {S}}, the above writes

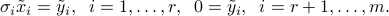
sigma_i tilde{x}_i = tilde{y}_i , ;; i = 1,ldots, r, ;; 0 = tilde{y}_i , ;; i=r+1,ldots,m.

Two cases can occur.

  • If the last 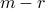m-r components of 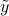tilde{y} are not zero, then the above system is infeasible, and the solution set is empty. This occurs when 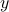y is not in the range of A.

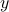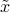  • If y is in the range of A, then the last set of conditions in the above system hold, and we can solve for tilde{x} with the first set of conditions:

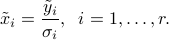
tilde{x}_i = frac{tilde{y}_i}{sigma_i} , ;; i = 1,ldots, r.

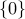The last n-r components of tilde{x} are free. This corresponds to elements in the nullspace of A. If A is full column rank (its nullspace is reduced to {0}), then there is a unique solution.

Pseudo-inverse

Definition

The solution set is conveniently described in terms of the pseudo-inverse of A, denoted by 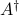A^dagger, and defined via the SVD of A:

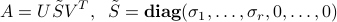
A = U tilde{ {S}} V^T, ;; tilde{ {S}} = mbox{bf diag}(sigma_1,ldots,sigma_r,0,ldots,0)

as one with same SVD, with non-zero singular values inverted, and the matrix 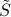tilde{S} transposed:

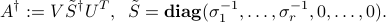
A^dagger := V tilde{ {S}}^dagger U^T, ;; tilde{ {S}} = mbox{bf diag}(sigma_1^{-1},ldots,sigma_r^{-1},0,ldots,0).

The pseudo-inverse of a matrix is always well-defined, and that it has the same size as the transpose 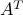A^T. When the matrix is invertible (it is square and full column or row rank: 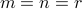m=n=r), then it reduces to the inverse.

Example: pseudo-inverse of a 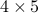4 times 5 matrix.

Matlab syntax
>> Adagger = pinv(A);

Link with solution set

From the above development, we see that the solution set can be written as

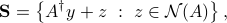
mathbf{S} = left{ A^dagger y + z ~:~ z in {cal N}(A) right},

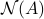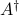where {cal N}(A) is the nullspace of A. Both A^dagger and a basis for the nullspace can be computed via the SVD.

Case when A is full rank

If A is full column rank, the pseudo-inverse can be written as

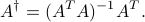
A^dagger = (A^TA)^{-1}A^T.

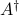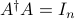In that case, A^dagger is a left-inverse of A, since A^dagger A = I_n.

If A is full row-rank, then the pseudo-inverse can be written as

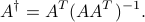
A^dagger = A^T(AA^T)^{-1}.

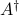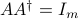In that case, A^dagger is a right-inverse of A, since AA^dagger = I_m.

Sensitivity analysis and condition number

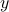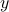Sensitivity analysis refers to the process of quantifying the impact of changes in the linear equations’ coefficients (the matrix A and vector y), on the solution. To simplify, let us assume that A is square and invertible, and analyze the effects of errors in y only. The condition number of the matrix A quantifies this.

We start from the linear equation above, which has the unique solution 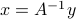x = A^{-1} y. Now assume that 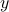y is changed into 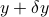y+delta y, where 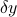delta y is a vector that contains the changes in 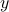y. Then let us denote by 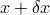x + delta x the new solution, which is 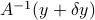A^{-1} (y + delta y). From the equations

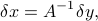
delta x = A^{-1} delta y, ;;

and via the definition of the largest singular value norm, we obtain:

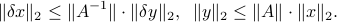
|delta x|_2 le |A^{-1}| cdot |delta y|_2 , ;; |y|_2 le |A| cdot |x|_2 .

Combining the two inequalities we obtain:

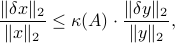
frac{|delta x|_2}{|x|_2} le kappa(A) cdot frac{|delta y|_2}{|y|_2} ,

where 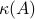kappa(A) is the condition number of A, defined as

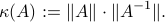
kappa(A) := |A| cdot |A^{-1}|.

We can express the condition number as the ratio between the largest and smallest singular values of A:

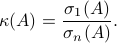
kappa(A) = frac{sigma_1(A)}{sigma_n(A)}.

The condition number gives a bound on the ratio between the relative error in the left-hand side to that of the solution. We can also analyze the effect of errors in the matrix itself on the solution. The condition number turns out to play a crucial role there as well.