Linear Equations: Definition and Main Issues
Definition
Link with subspaces and affine sets
Issues with linear equations
Definition
A linear equation in  is an equation of the form
is an equation of the form
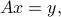
where 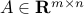 and
and 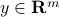 are given. Linear equations arise in many areas of engineering. (Note that a more rigorous terminology would call the above equation an affine equation, except in the special case
are given. Linear equations arise in many areas of engineering. (Note that a more rigorous terminology would call the above equation an affine equation, except in the special case  .)
.)
Example:
We define the solution set to be simply the set of solutions to the linear equation:

This is a subset of 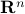 , where
, where 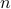 is the column size of
is the column size of  .
.
Link with subspaces and affine sets
Recall the definition of an affine set as the span of a collection of vectors, possibly translated away from the origin. It turns out that solutions sets of linear equations are always affine (Proof).
The relationship between linear equations and affine sets goes both ways: any affine set can be expressed as the solution set of some linear equation. Thus, the study of linear equations will help us understand basic geometric concepts such as subspaces and affine sets. In addition, we now know how to parametrize affine sets in two ways: either as the translated span of vectors, or as the solution set of a linear equation 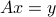 .
.
Example: hyperplane.
Important issues
Several important issues arise with linear equations.
Existence
First, do solutions exist? This question leads to the notion of range of a matrix, which characterizes those vectors 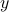 for which solutions exist. The notion of rank allows to determine the dimension of the affine set of solutions. If there are no solutions, we can try to solve the equation in approximate manner: this is what least-squares solutions, examined later, are about.
for which solutions exist. The notion of rank allows to determine the dimension of the affine set of solutions. If there are no solutions, we can try to solve the equation in approximate manner: this is what least-squares solutions, examined later, are about.
Unicity
Next we may be interested in the question of unicity of solutions (if any). The nullspace associated with  allows to describe the set of solutions, and characterizes the ambiguity about solutions. When the solution is not unique, we say that the system is undetermined.
allows to describe the set of solutions, and characterizes the ambiguity about solutions. When the solution is not unique, we say that the system is undetermined.
The notion of nullspace allows to characterize systems for which the solution, if it exists, is unique. If there are many solutions, we can then define the notion of minimum-norm solution.
Solution concepts
If the solution set is empty, that is, the equation does not have any solution, then we may find an approximate solution by solving an optimization problem.
If the equation has many solutions to choose from, we can find a particular solution. The one with minimum norm is often of practical interest.
Sensitivity
A linear equation is often obtained from measurement data. In practice, the ‘‘data’’ in the equation (the matrix  and vector
and vector 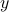 in the linear equation
in the linear equation 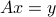 ) can be noisy.
) can be noisy.
Sensitivity analysis is concerned with the study of the impact of errors in 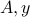 , on a solution
, on a solution  . The linear algebra methods developed in the first part of this course allow to deal with noise in the measurement vector
. The linear algebra methods developed in the first part of this course allow to deal with noise in the measurement vector 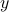 . The analysis of the impact of noise in the matrix
. The analysis of the impact of noise in the matrix  is usually more difficult.
is usually more difficult.
 system
system