Solution Concepts
Solution set
Least-norm solutions
Approximate solutions
Solution set
We consider the linear equation
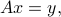
where 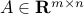 and
and 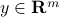 are given.
The associated solution set is the set of solutions
are given.
The associated solution set is the set of solutions

By construction, it is an affine set of 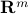 .
.
Several cases may occur:
If
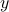 is in the range of
is in the range of  , the equation has at least a solution, and the solution set is not empty. If the nullspace is not
, the equation has at least a solution, and the solution set is not empty. If the nullspace is not 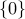 , then this solution is not unique. In this case, we develop the notion of minimum-norm solution, which allows to select a particular solution among the many.
, then this solution is not unique. In this case, we develop the notion of minimum-norm solution, which allows to select a particular solution among the many.If
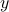 is not in the range of
is not in the range of  , then there are no solutions: the solution set is empty. In this case we introduce the notion of approximate solution, which is based on minimizing the norm of the ‘‘residual error’’
, then there are no solutions: the solution set is empty. In this case we introduce the notion of approximate solution, which is based on minimizing the norm of the ‘‘residual error’’ 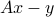 . We refer to a vector
. We refer to a vector  that minimizes this error in norm, as a minimum-residual solution (although, strictly speaking, it is not a solution to the original equation).
that minimizes this error in norm, as a minimum-residual solution (although, strictly speaking, it is not a solution to the original equation).
For both the minimum-norm and minimum-residual problems, the qualitative behavior of the solution depends crucially on the norm used to measure the size of the vectors involved.
Minimum-norm solutions
In the case when  , there may be many solutions to the linear equation
, there may be many solutions to the linear equation 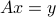 , namely if and only if the nullspace of
, namely if and only if the nullspace of  is not reduced to
is not reduced to 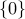 . It is then of interest to select a specific solution. A popular choice is the minimum-norm solution, obtained via the optimization problem
. It is then of interest to select a specific solution. A popular choice is the minimum-norm solution, obtained via the optimization problem

Again, the qualitative behavior of the solution depends heavily on the choice of the norm used. Depending on the choice for the norm  , such problems may or may not be easy to solve. For the popular norms (
, such problems may or may not be easy to solve. For the popular norms (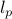 , with
, with  ), they are.
), they are.
A popular choice corresponds to the case when the norm in the objective function of the above problem is the Euclidean norm. When  is full row rank, meaning that there is always a solution irrespective of
is full row rank, meaning that there is always a solution irrespective of 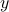 , the minimum-Euclidean-norm solution has a closed-form expression
, the minimum-Euclidean-norm solution has a closed-form expression

(Note that the inverse exist, since  is full row rank.) The geometric interpretation of this solution is that it is the projection of
is full row rank.) The geometric interpretation of this solution is that it is the projection of 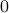 on the set of solutions to the linear equation.
on the set of solutions to the linear equation.
Example: Control of a unit mass.
Other norms are often used. For example, the 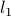 norm is often used as it tends to produce sparse solution vectors
norm is often used as it tends to produce sparse solution vectors  , meaning a vector
, meaning a vector  which has many zero components. This is in turn useful when one is trying to achieve some desired target
which has many zero components. This is in turn useful when one is trying to achieve some desired target 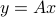 by proper choice of
by proper choice of  , with the smallest number of non-zero components.
, with the smallest number of non-zero components.
Example: Sparse image compression.
Approximate solutions via residual error minimization
Basic idea
When 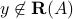 , there exist no solutions to the equation
, there exist no solutions to the equation 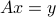 . This can be due to several factors: the linear equation may be an approximation of a non-linear one, resulting in model errors; or
. This can be due to several factors: the linear equation may be an approximation of a non-linear one, resulting in model errors; or 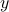 might be a noisy measurement of the output of some linear process, resulting in measurement errors; or both. Such errors might make the solution set empty.
might be a noisy measurement of the output of some linear process, resulting in measurement errors; or both. Such errors might make the solution set empty.
We can then try to find an approximate solution, by minimizing the distance from 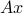 to
to 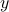 by proper choice of
by proper choice of  . We are led to problems of the form
. We are led to problems of the form

Again, the ‘‘solution’’ found this way depends heavily on the choice of norm. Also that choice has an impact on the computational complexity of the optimization problem above. As before for the popular norms (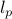 , with
, with  ), these problems are easy.
), these problems are easy.
Least-squares
The most well-known case corresponds to the choice of the 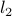 (Euclidean) norm, because it is the only one of the three which leads to a closed-form solution. The corresponding problem
(Euclidean) norm, because it is the only one of the three which leads to a closed-form solution. The corresponding problem

is called a least-squares problem. We will see later that, when  is full column rank, the problem has a unique, closed-form solution, which is in the form
is full column rank, the problem has a unique, closed-form solution, which is in the form

Examples:
Other norms
Other norms are often used. For example one can experimentally observe that using the 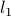 norm tends to produce solutions such that
norm tends to produce solutions such that  for many
for many 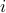 's: the residual error vector
's: the residual error vector 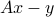 is sparse (has many zero elements). Solving the corresponding problem can be efficiently done, but no ‘‘closed-form’’ solution is known, so we must use optimization solvers. We examine the corresponding problem here.
is sparse (has many zero elements). Solving the corresponding problem can be efficiently done, but no ‘‘closed-form’’ solution is known, so we must use optimization solvers. We examine the corresponding problem here.