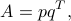Rank-one matrices: a representation theorem
We prove the theorem mentioned here:
Proof: For any non-zero vectors 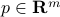 ,
, 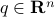 , the matrix
, the matrix 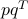 is indeed of rank one: if
is indeed of rank one: if  , then
, then

When  spans
spans 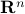 , the scalar
, the scalar  spans the entire real line (since
spans the entire real line (since  ), and the vector
), and the vector  spans the subspace of vectors proportional to
spans the subspace of vectors proportional to 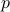 . Hence, the range of
. Hence, the range of 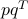 is the line
is the line

which is of dimension  .
.
Conversely, if  is of rank one, then its range is of dimension one, hence it must be a line passing through
is of rank one, then its range is of dimension one, hence it must be a line passing through  . Hence for any
. Hence for any  there exist a function
there exist a function  such that
such that

Using  , where
, where 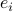 is the
is the 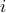 -th vector of the standard basis, we obtain that there exist numbers
-th vector of the standard basis, we obtain that there exist numbers  such that for every
such that for every 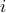 :
:

We can write the above in a single matrix equation:

(Indeed, the previous equation is the above, written column by column.)
Now letting  , and realizing that the matrix
, and realizing that the matrix  is simply the identity matrix, we obtain
is simply the identity matrix, we obtain

as desired.
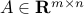 can be written as an ‘‘outer product’’, or
can be written as an ‘‘outer product’’, or