Robust Least-Squares
We start from the least-squares problem:

where 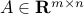 ,
, 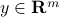 .
.
Now assume that the matrix  is imperfectly known. A simple model is to assume that the matrix is only known to be within a certain ‘‘distance’’ (in matrix space) to a given ‘‘nominal’’ matrix
is imperfectly known. A simple model is to assume that the matrix is only known to be within a certain ‘‘distance’’ (in matrix space) to a given ‘‘nominal’’ matrix 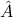 . Precisely, let us assume that assume
. Precisely, let us assume that assume  , where
, where  denotes the largest singular value norm, and
denotes the largest singular value norm, and  measures the size of the uncertainty. We now address the robust least-squares problem:
measures the size of the uncertainty. We now address the robust least-squares problem:

The interpretation of this problem is that it is trying to minimize the worst-case value of the residual norm.
For fixed  , and using the fact that the Euclidean norm is convex, we have
, and using the fact that the Euclidean norm is convex, we have

By definition of the largest singular value norm, and given our bound on the size of the uncertainty, we have

Thus, we have a bound on the objective value of the robust problem:

It turns out that the upper bound is attained by some choice of the matrix  , specifically:
, specifically:

Hence the robust least-squares is equivalent to the problem

The above is an SOCP:

As given, this SOCP can be solved using SVD methods. However, problems involving constraints (such as sign constraints on  ) cannot be solved by SVD, while they still can be solved with SOCP.
) cannot be solved by SVD, while they still can be solved with SOCP.