Least-Squares Design
Example data
Least-squares approach
Data and example
Trade-off curve
Example data
For our particular example, we have the following parameters:
Number of antennas:
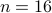 .
.Wavelength:
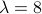 .
.Pass-band size:
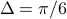 .
In what follows, we use the following matlab applet to define the data of our problem.
.
In what follows, we use the following matlab applet to define the data of our problem.
N = 10; % discretization parameter n = 16; % number of antennas lambda = 8; % wavelength Phi = pi/6; % sidelobe parameter
Least-squares approach
We examine how least-squares can be used to strike a trade-off between the sideloble level attenuation and thermal noise power. The initial problem reads
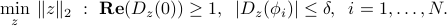
The basic idea is to penalize the constraints, as follows: we choose a ‘‘trade-off parameter’’ 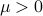 and solve the problem
and solve the problem
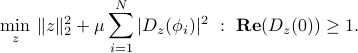
Remember that the function 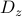 is linear in
is linear in  :
:
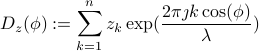
Hence, the above problem is a linearly constrained least-squares problem.
CVX implementation
The above problem can be solved via linear algebra (SVD) methods. Here, we do not even bother to invoke SVD — CVX will do. A CVX implementation of this problem is given below. Note how we use a new vector variable to handle the objective function. Note also that CVX understands complex variables.
Angles = linspace(Phi,pi,N); % angles in the stop band
a = 2*pi*sqrt(-1)/lambda; % intermediate parameter
cvx_begin
variable z(n,1) complex;
variable r(N,1) complex;
minimize( z'*z+mu*r'*r )
subject to
for i = 1:N,
exp(a*cos(Angles(i))*(1:n))*z == r(i);
end
real( exp(a*(1:n))*z) >= 1;
cvx_end
Note that the penalty approach adopted here will not enforce the desired constraints. We can only hope that, for 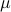 large enough, all of the terms in the sum will go below the desired threshold
large enough, all of the terms in the sum will go below the desired threshold 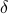 . In practice, we expect that some terms might not. It seems to be hard to achieve the best trade-off this way. The following plot shows the trade-off curve that we can achieve.
. In practice, we expect that some terms might not. It seems to be hard to achieve the best trade-off this way. The following plot shows the trade-off curve that we can achieve.
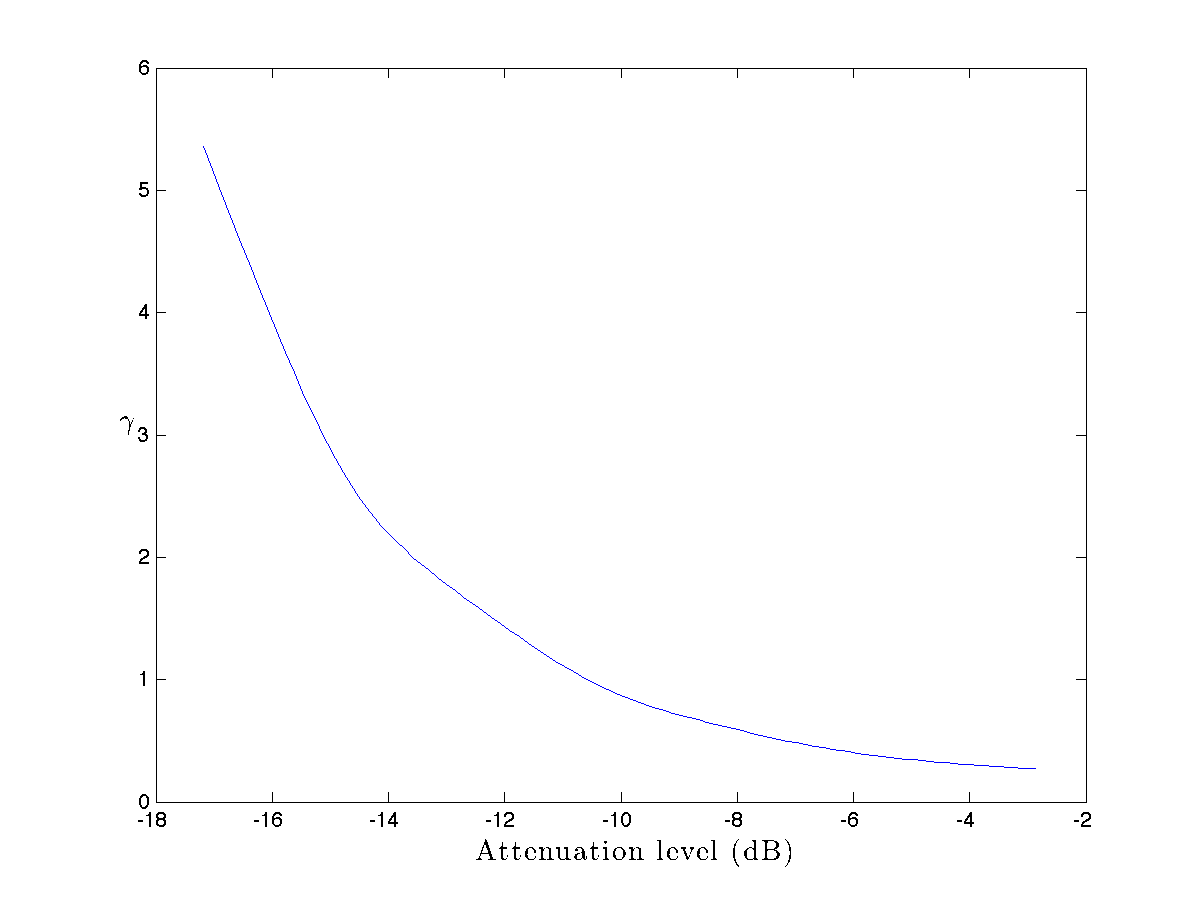 |
Trade-off curve achieved via via least-squares. |
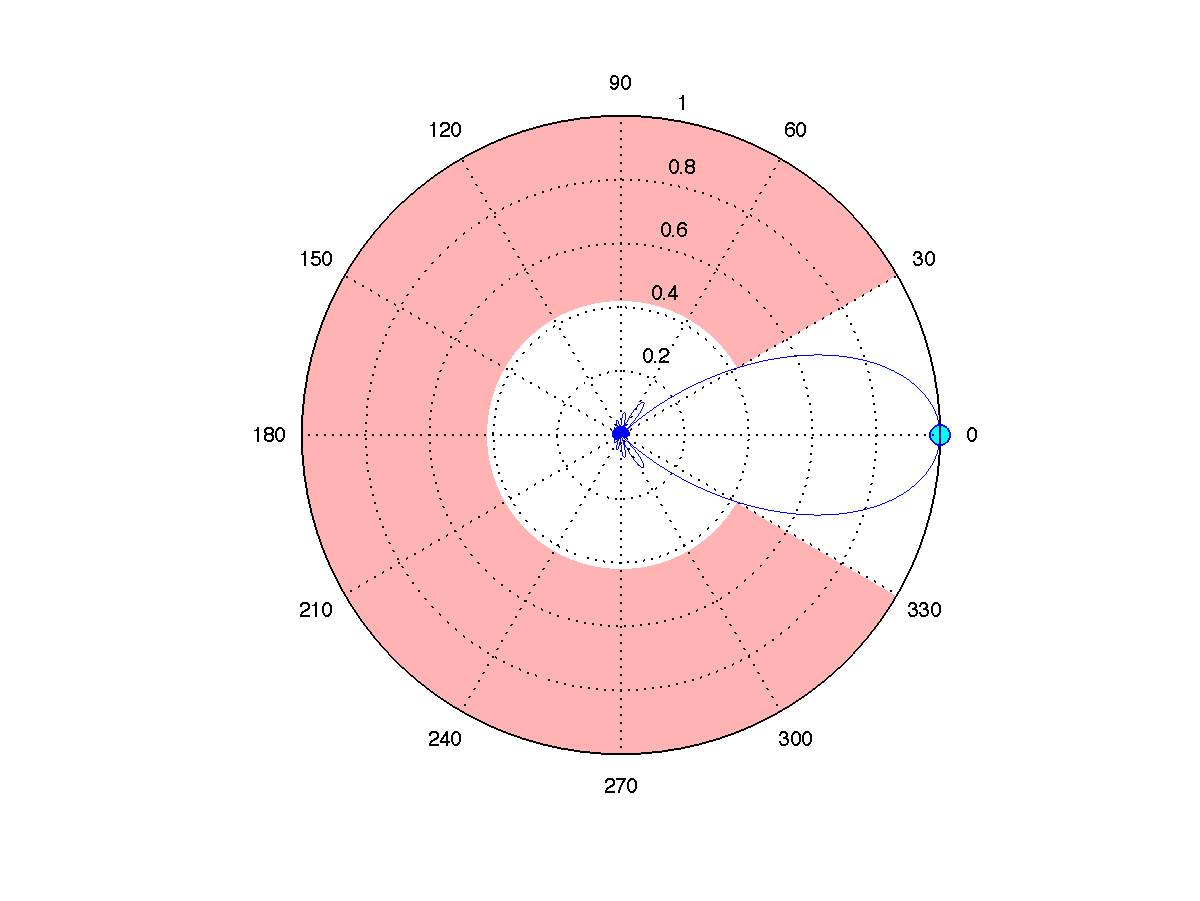
 points, with trade-off parameter
points, with trade-off parameter 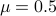 . The corresponding sidelobe attenuation level is
. The corresponding sidelobe attenuation level is 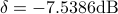 , and the thermal noise power is
, and the thermal noise power is 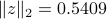 .
.