Digital Circuit Design: GP Model

Generalized posynomial model
Explicit posynomial model

Generalized Posynomial Representation

We now consider the problem of choosing the scale factors to minimize the total delay, subject to an area constraint.

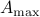$min_{x} : D(x) ~:~ A_i(x) le A_{rm max}, ;; x_i ge 1, ;; i=1,ldots, n,$

where $A_{rm max}$ is an upper bound on the area of each gate.

Since 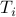T_i is a maximum of function of 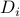D_i , itself a posynomial in , we can express the total delay as a posynomial in . Hence the above is a GP.

Explicit Posynomial Representation

Let us form the GP in a more explicit way, using the intermediate variables 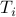T_i , which we encountered in our definition of the delay. The basic idea is to replace the equality defining these intermediate variables, e.g.

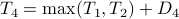
by inequalities:

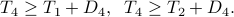
It turns out we ‘‘loose nothing’’ in this process; that is, at optimum, equality holds.

Mor generally, we replacing the constraint

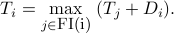
$T_i = max_{j in mbox{small FI(i)}} : (T_j + D_i).$

by a relaxed version:

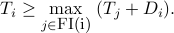
$T_i ge max_{j in mbox{small FI(i)}} : (T_j + D_i) .$

The above can be written:

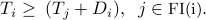
$T_i ge : (T_j + D_i) , ;; j in mbox{small FI(i)}.$

We obtain an explicit representation of the previous GP:

$min_{x,T>0} : D ~:~ begin{array}[t]{l} A_i(x) le A_{rm max}, ;; x_i ge 1, ;; i=1,ldots, n, D ge T_i, ;; i=1,ldots, n, T_i ge (T_j + D_i(x)), ;; i=1,ldots, n, ;; j in mbox{small FI(i)}. end{array}$

The above is also a GP. At the expense of adding new variables and also adding constraints, we have obtained a sparser problem.