Inner Approximations
Inner spherical approximation
Inner box approximation
Inner spherical approximation
We first focus on the problem of finding the largest radius of a sphere contained in the intersection. It is easy to check that a sphere of center 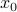 and radius
and radius 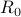 is contained in a sphere of center
is contained in a sphere of center 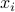 and radius
and radius 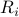 if and only if the differences in the radiuses exceeds the distance between the centers:
if and only if the differences in the radiuses exceeds the distance between the centers:
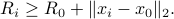
Our inner approximation problem then becomes the SOCP
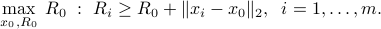
We note that the measurements are inconsistent if and only if at optimum, 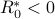 . This is the same as saying that there is no point
. This is the same as saying that there is no point 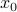 which satisfies the constraints
which satisfies the constraints 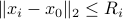 ,
, 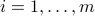 .
.
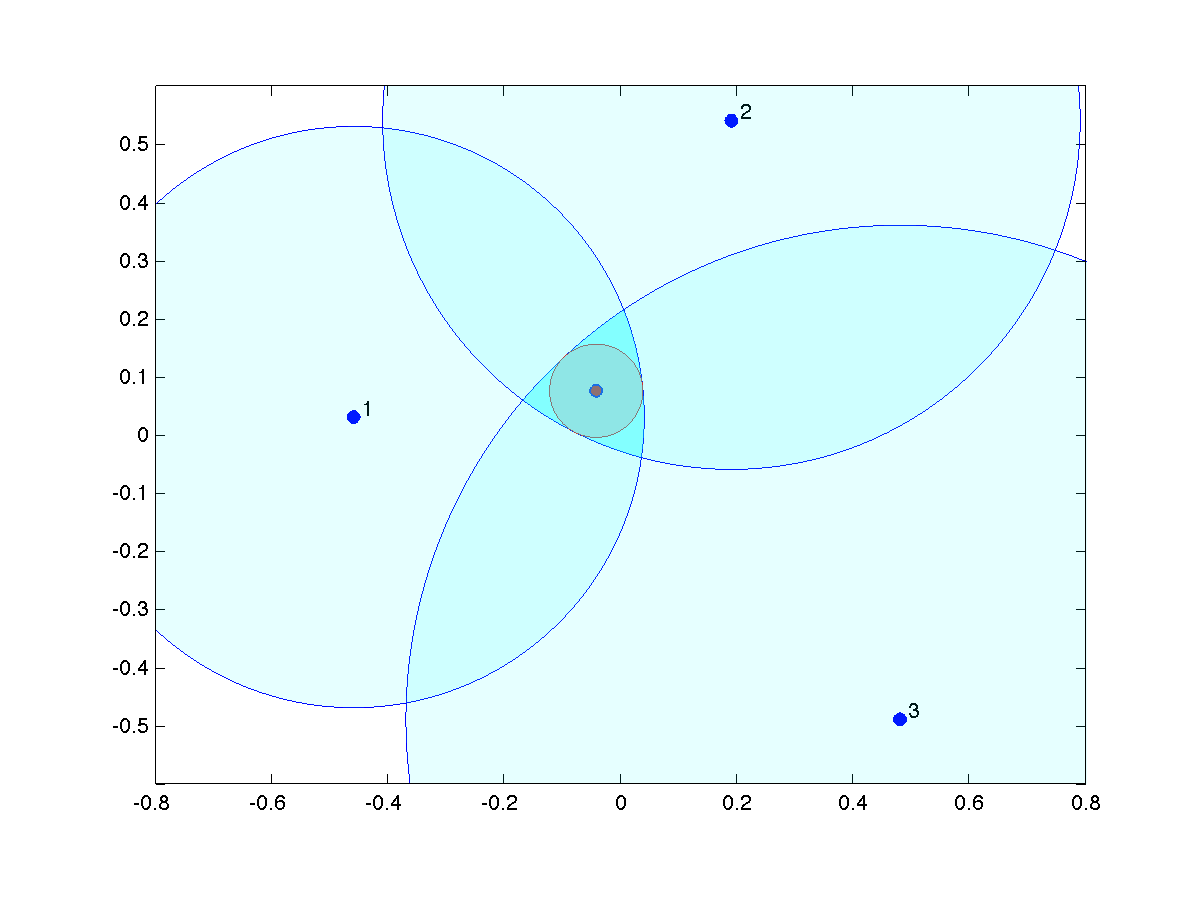 |
Inner spherical approximation to the intersection. This provides an estimated point (the center of the inner shpere), with an optimistic estimate of the uncertainty around it. |
Inner box approximation
We can also consider the problem of finding the largest box inside the intersection. We simply ensure that the vertices of a box with size 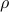 are inside the intersection, and then maximize
are inside the intersection, and then maximize 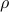 . In 2D or 3D, this is easy, as there is a moderate number of vertices. The problem is written
. In 2D or 3D, this is easy, as there is a moderate number of vertices. The problem is written
In the above,  is the number of vertices of the box (
is the number of vertices of the box ( in 2D,
in 2D, 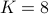 in 3D), and
in 3D), and 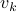 ,
, 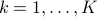 are the vertices of the unit box, that is, the vectors with elements
are the vertices of the unit box, that is, the vectors with elements 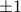 .
.
