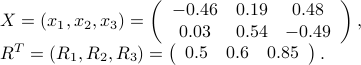Problem Statement
The localization problem
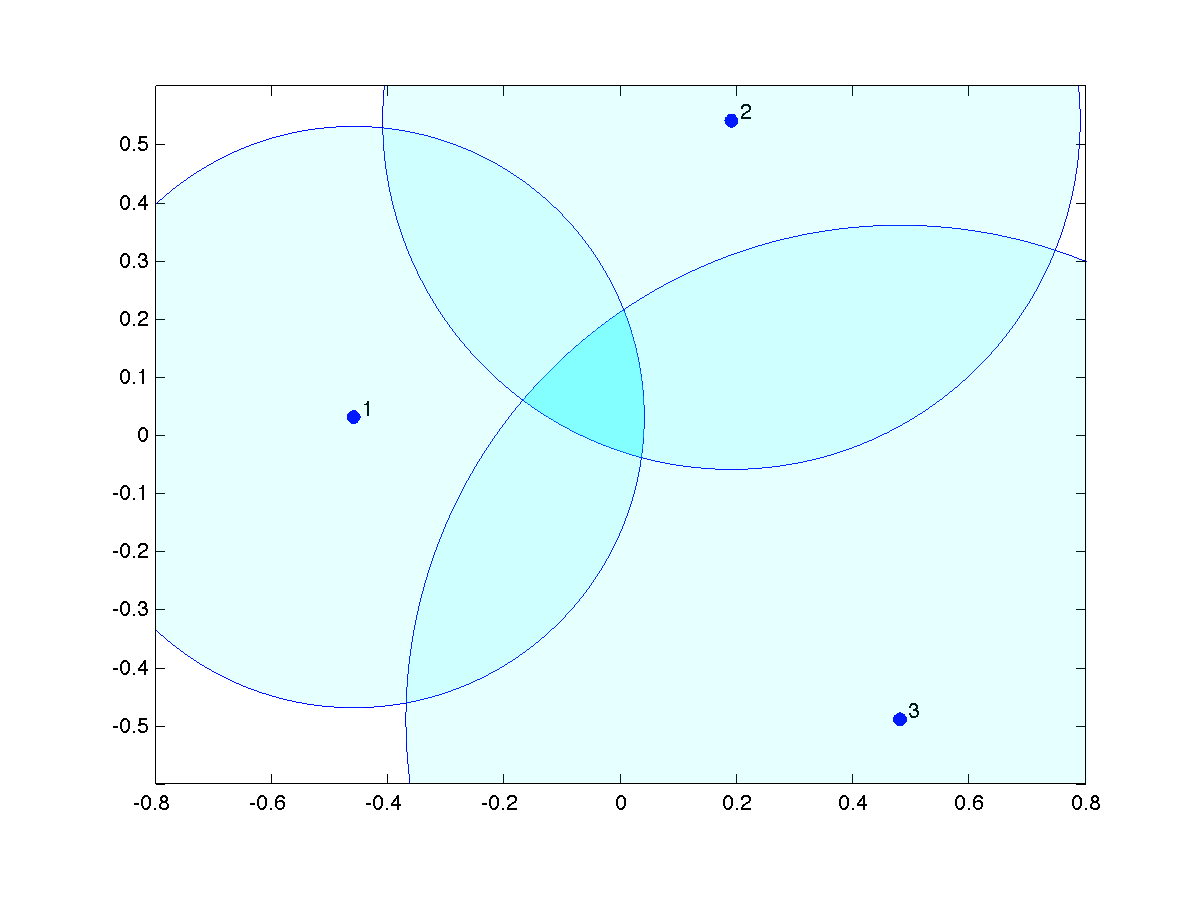
We are given anchor positions 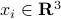 , and associated distances from these anchor points to an unknown object,
, and associated distances from these anchor points to an unknown object, 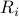 ,
,  . The problem is to estimate a position of the object, and associated measure of uncertainty around the estimated point. Geometrically, the measurements imply that the object is located at the intersection of the
. The problem is to estimate a position of the object, and associated measure of uncertainty around the estimated point. Geometrically, the measurements imply that the object is located at the intersection of the 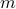 spheres of centers
spheres of centers 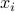 and radiuses
and radiuses 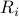 ,
,  . The main problem is to provide one point in the intersection located at some kind of ‘‘center’’, and also a measure of the size of the intersection.
. The main problem is to provide one point in the intersection located at some kind of ‘‘center’’, and also a measure of the size of the intersection.
Issues to be addressed
In general, the measurements may not be consistent, in the sense that the intersection of all the spheres may be empty. We will first address the problem of checking consistency, and adjust our measurements if necessary. Assuming then the measurements to be consistent, so that the spheres do intersect, in general the intersection may not be reduced to a unique point, which means that the measurement only allow to estimate the position with some level of uncertainty. We aim to provide both an estimate of the position, and a measure of the uncertainty.
There are two approaches to this problem. One consists in finding an inner approximation to the intersection, which is the largest sphere (or box) contained in it. This is in a sense an ‘‘optimistic’’ approach. Another approach is ‘‘pessimistic’’ and consists in finding the smallest sphere (or box) that contains the intersection. In both cases, the optimal radius of the sphere (or size of box) is a measure of uncertainty, and its center is the estimated position.