LP Relaxations of Boolean Problems
Boolean problems
LP relaxation
When is the LP relaxation exact?
Examples
Boolean problems
A Boolean optimization problem is one where the variables are constrained to be Boolean. An example of Boolean problem is the so-called Boolean LP

Such problems are usually very hard to solve exactly: this would require a complete enumeration of all the exponential number of possible points in  .
.
LP relaxation
The LP relaxation takes the form

The relaxation provides a lower bound on the original problem:  . Hence, its optimal points may not be feasible (not Boolean). Even though a solution of the LP relaxation may not necessarily be Boolean, we can often interpret it as a {em fractional} solution to the original problem. For example, in a graph coloring problem, the LP relaxation colors the nodes of the graph not with a single color, but with many.
. Hence, its optimal points may not be feasible (not Boolean). Even though a solution of the LP relaxation may not necessarily be Boolean, we can often interpret it as a {em fractional} solution to the original problem. For example, in a graph coloring problem, the LP relaxation colors the nodes of the graph not with a single color, but with many.
Exact solutions
Boolean problems are not always hard to solve. Indeed, in some cases, one can show that the LP relaxation provides an exact solution to the Boolean problem, as optimal points turn out to be Boolean. A few examples in this category:
Weighted bipartite matching
The weighted bipartite matching problem is to match 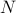 people to
people to 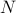 tasks, in a one-to-one fashion. The cost of matching person
tasks, in a one-to-one fashion. The cost of matching person 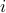 to task
to task 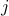 is
is 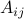 . The problem reads
. The problem reads

Shortest path
The shortest path problem has the form

where  stands for the incidence matrix of the network, and arcs with
stands for the incidence matrix of the network, and arcs with 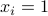 form a shortest forward path between nodes
form a shortest forward path between nodes  and
and 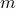 . As before the LP relaxation in this case is exact, in the sense that its solution is Boolean. The shortest path problem can be solved very efficiently with specialized algorithms based on the LP relaxation to the above formulation.
. As before the LP relaxation in this case is exact, in the sense that its solution is Boolean. The shortest path problem can be solved very efficiently with specialized algorithms based on the LP relaxation to the above formulation.