Network Flows

LP and QP > Applications> Back | Networks | Next

Network models
Minimum cost network flow

Network models

What is a network?

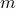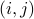We return to the network model described here. We consider a network (directed graph) having nodes connected by directed arcs (ordered pairs (i,j) ). We assume there is at most one arc from node 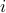to node 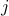, and no self-loops. We define the arc-node incidence matrix 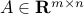$A in mathbf{R}^{m times n}$ to be the matrix with coefficients $A_{ij} = 1$ if arc 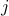starts at node 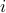, 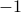if it ends there, and 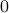otherwise. 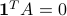Note that the column sums of are zero: $mathbf{1}^T A = 0$ .

The figure shows the graph associated with the arc-node incidence matrix

A = left[begin{array}{cccccccc} 1 & 1 & 0 & 0 & 0 & 0 & 0 & -1 -1 & 0 & 1 & 0 & 0 & 0 & 0 & 1 0 & -1 & -1 & -1 & 1 & 1 & 0 & 0 0 & 0 & 0 & 1 & 0 & 0 & -1 & 0 0 & 0 & 0 & 0 & 0 & -1 & 1 & 0 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 end{array}right] .

Flows

A flow (of traffic, information, charge) is represented by a vector $x in mathbf{R}^n$ , and the {em total flow leaving node 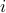} is then $(Ax)_i = sum_{j=1}^n A_{ij} x_j$ .

Minimum cost network flow

The minimum cost network flow problem has the LP form

min_x : c^Tx ~:~ Ax = b, ;; l le x le u,

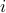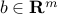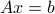where c_i is the cost of flow through arc , l,u provide upper and lower bounds on and $b in mathbf{R}^m$ is an external supply vector. This vector may have positive or negative components, as it represents supply and demand. We assume that $mathbf{1}^Tb = 0$ , so that the total supply equals the total demand. The constraint Ax=b represents the balance equations of the network.

Maximum flow

A more specific example is the max flow problem, where we seek to maximize the flow between node (the source) and node 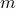(the sink). It bears the form

$min_{x,t} : t ~:~ Ax = te, ;; l le x le u,$

with e = (1,0,ldots,0,-1) .