Mean-Variance Trade-Off in Portfolio Optimization
Portfolio optimization with sign constraints
We return to the portfolio optimization problem. This time, we assume that shorting is not allowed. In other words, we can only invest in any given asset, or decide not to invest; but we can't borrow and hold any negative position. The problem we have introduced now takes the form

where 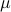 is our target for the nominal return, and
is our target for the nominal return, and 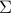 is a positive semi-definite matrix that contains information about the uncertainty on the assets’ returns (see here). The above is a QP.
is a positive semi-definite matrix that contains information about the uncertainty on the assets’ returns (see here). The above is a QP.
cvx_begin
variable x(n,1);
minimize( x'*S*x );
subject to
rhat'*x == mu;
x >= 0;
cvx_end
Other constraints
We can add other linear or affine inequality constraints to the problem.
Sector bounds
For example, we can put upper bounds on some elements of  , to limit the amount of investment in any single asset. We can also require that the total sum invested in a given sector (corresponding to say, the first
, to limit the amount of investment in any single asset. We can also require that the total sum invested in a given sector (corresponding to say, the first 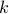 assets) does not exceed a fraction
assets) does not exceed a fraction 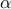 of the total sum invested. This can be modeled by
of the total sum invested. This can be modeled by

Again, the above is a QP, with just one more affine inequality.
Diversification
We can also impose some diversification constraints. For example, we may impose that no group of 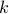 (with
(with  ) assets contain more than
) assets contain more than  of the total invested. We write this as
of the total invested. We write this as
![s_k(x) := sum_{i=1}^k x_{[i]} le 0.8 sum_{i=1}^n x_i,](eqs/5909999965544865798-130.png)
where ![x_{[i]}](eqs/2760541963639494573-130.png) is the
is the 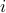 -th largest component of
-th largest component of  , so that
, so that  is the sum of the
is the sum of the 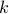 largest elements in
largest elements in  . The function
. The function  is convex, since it is the point-wise maximum of linear functions (hence it is polyhedral):
is convex, since it is the point-wise maximum of linear functions (hence it is polyhedral):

The function  is implemented in CVX by invoking sum_largest.
is implemented in CVX by invoking sum_largest.
cvx_begin
variable x(n,1);
minimize( x'*S*x );
subject to
rhat'*x == mu;
x >= 0;
sum_largest(x,10) <= 0.8*sum(x);
cvx_end
The above expression for  simply states that the function
simply states that the function  is the pointwise maximum of the
is the pointwise maximum of the  (
( choose
choose 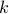 ) linear functions obtained by choosing any subset of
) linear functions obtained by choosing any subset of 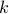 indices in
indices in  . For example, with
. For example, with 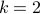 and
and  :
:

Since  is polyhedral, we can definitely represent the constraint
is polyhedral, we can definitely represent the constraint  as a finite set of affine inequality constraints, that is, a polyhedron. However the list of constraints is huge: for
as a finite set of affine inequality constraints, that is, a polyhedron. However the list of constraints is huge: for 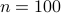 ,
,  , we have to list more than
, we have to list more than  constraints!
constraints!
A more efficient way is based in the following expression, proven here:

In this form, the diversification constraint can be expressed as: there exist a scalar 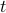 and a
and a  -vector
-vector  such that
such that

In the above, 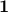 is the vector of ones in
is the vector of ones in 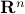 . Here,
. Here,  are additional variables that allow a QP representation with a moderate number of variables and constraints:
are additional variables that allow a QP representation with a moderate number of variables and constraints:
![min_{u,t,x} : x^TSigma x ~:~ begin{array}[t]{l} hat{r}^Tx = mu, ;; x ge 0, kt + displaystylesum_{i=1}^n u_i le 0.8 displaystylesum_{i=1}^n x_i, u ge 0, ;; u ge x- t mathbf{1}. end{array}](eqs/8471739407613132694-130.png)
The lesson here is that a polyhedron in a  -dimensional space, with an exponential number of facets, can be represented as a polyhedron in a higher dimensional space (in our case, with dimension
-dimensional space, with an exponential number of facets, can be represented as a polyhedron in a higher dimensional space (in our case, with dimension  ), with a moderate number of facets (precisely
), with a moderate number of facets (precisely  facets). By adding just a few dimensions to the problem we are able to deal (implicitly) with a very high number of constraints.
facets). By adding just a few dimensions to the problem we are able to deal (implicitly) with a very high number of constraints.