Filter Design

LP and QP > Applications > Back | Filter design

Finite impulse response filters
A design problem
LP formulation

Finite Impulse Response filters

Filters

A singel-input, single-output filter is a dynamical system, with input a signal with values in u(t) in mathbf{R}

, and output another signal with values y(t) in mathbf{R}

. Here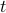

stands for the (discrete) time variable.

Finite impulse response filter

A finite-impulse response (FIR) filter is a particular type of filter which has the form

$y(t) = sum_{i=0}^{n-1} h_i u(t-i), ;; t in Z.$

The vector $h=(h_0,ldots,h_{n-1}) in mathbf{R}^n$ is called the impulse response of the filter. Its name derives from the fact that the response of the filter above to the so-called impulse

$y(t) =left{ begin{array}{ll} h_t & mbox{if } 0 le t le n-1, 0 & mbox{otherwise.} end{array}right.$

Frequency response

The Fourier transform of the impulse response is a complex-valued function H : mathbf{R} rightarrow mathbf{C}

with values

$H(omega)= sum_{t=0}^{n-1} h_t e^{-jmath omega t} .$

This function is of importance, since it dictates how the filter responds to periodic signals. Precisely, if the input is a complex exponential $u(t) = e^{jmath omega t}$ , then the output will be the scaled complex exponential y(t) = H(omega) u(t)

Example: Moving average filter. An example of a FIR filter is a moving average filter. The moving average filter of length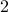

is of the form

$y(t) = frac{1}{2} ( u(t) + u(t-1) ), ;; t in mathbf{R}.$

Linear-phase FIR filters

Linear phase FIR filters turns out to be simpler to design. Such filters involves an odd number of taps: n = 2N+1

, with an impulse response that is symmetric around the midpoint:

The qualifier linear phase comes from the fact that, for such filters, the frequency response bears the form

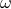$H(omega) = e^{-jmath omega N} tilde{H}(omega),$

$tilde{H}(omega) := 2h_0cos(Nomega) + 2 h_1 cos((N-1)omega) + ldots + h_N.$

A design problem

A design problem involving FIR filters typically involves the FIR filter's impulse response as a variable. The goal is to adjust the response of the filter under a variety of inputs.

For example, we would like to ensure that the filter rejects high-frequency signals, but amplifies low-frequency ones to a certain degree. These two requirements involve the magnitude of the filter's frequency response.

where

is a ‘‘stop-band’’ frequency bound and delta_2

corresponds to an attenuation level we seek to achieve at high frequencies.

where

is a ‘‘pass-band’’ frequency bound and delta_1

corresponds to a lower bound on the amplification level that we seek to achieve at low frequencies.

The first constraint is convex in the design variable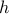

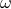. The second is not. In addition, both constraints actually involve an {em infinite} number of constraints, one for each frequency omega

LP formulation

Issue of non-convexity

To address the issue of non-convexity, we restrict our search for filters, to filters that are linear-phase. In that case, the magnitude of the frequency response can be written as

where now

is a real number. Without loss of generality, we can choose the impulse response vector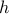

to be such that tilde{H}(0) >0

. Then the pass-band constraint

$delta_1 le tilde{H}(omega), ;; 0 le omega le Omega_p,$

which is now convex in the design variable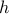

. In fact, it is an infinite number of affine inequalities, of the form

Frequency discretization

To address the issue of an infinite number of constraints, we simply discretize the frequency domain. Instead of enforcing the constraints for every frequency in an interval, we simply enforce them on a finite set inside the interval.

Let use choose a finite set of frequencies omega_i

that belong to the high-frequency region [Omega_s,+infty]

. The stop-band constraint is now approximated by the {em finite} number of affine inequalities in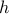

Likewise we choose another set of frequencies omega_i

that belong to the low-frequency region [0,Omega_p]

. The pass-band constraint is also approximated by a finite number of affine inequalities in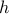

Together, the constraints can be written as h in {cal P}

, where ${cal P} subseteq mathbf{R}^n$ is a polytope.

Variant: pass-band ripple minimization

A variant for the above is to consider both a lower and upper bound on the low-frequency response. Often it is desirable to have a low pass-band ripple, which is a measure on the “flatness” of the frequency response's magnitude at low frequencies. A ripple level of delta_1

is enforced via the constraint

Trade-off curves

Based on these constraints, we may plot the trade-off curve between high-frequency attenuation against low-frequency amplification.