Tractable Cases

Robust LP > Motivations and standard forms | Tractable cases | Applications

Scenario models
Box uncertainty models
Ellipsoidal models

Scenario uncertainty

Uncertainty model

In the scenario uncertainty model, the uncertainty on a coefficient vector is described by a finite set of points:

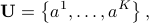
$mathbf{U} = left{ a^1,ldots,a^K right},$

where each vector 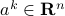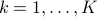$a^k in mathbf{R}^n$ , k=1,ldots,K corresponds to a particular “scenario”.

The robust counterpart to a half-space constraint:

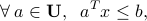
$forall : a in mathbf{U} , ;; a^Tx le b ,$

can be simply expressed as a set of 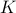affine inequalities:

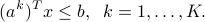
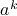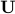Note that the scenario model actually enforces more than feasibility at the “scenario” points a^k . In fact, for any that is in the convex hull of the set mathbf{U} , the robust counterpart holds. Indeed, if the above holds, then for any set of nonnegative weights 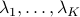lambda_1,ldots,lambda_K summing to one, we have

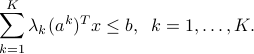
$sum_{k=1}^K lambda_k (a^k)^Tx le b, ;; k=1, ldots,K.$

With a scenario uncertainty, the robust counterpart to the original LP:

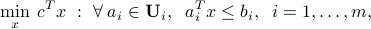
$min_x : c^Tx ~:~ forall : a_i in mathbf{U}_i , ;; a_i^Tx le b_i , ;; i= 1,ldots,m,$

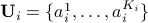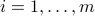with $mathbf{U}_i = { a_i^1,ldots,a_i^{K_i}}$ , i=1,ldots,m , becomes

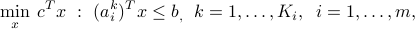
min_x : c^Tx ~:~ (a_i^k)^Tx le b_, ;; k=1, ldots,K_i, ;; i= 1,ldots,m,

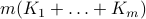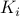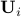This is an LP, with a total of m(K_1+ldots+K_m) constraints, where K_i is the number of elements in the finite set $mathbf{U}_i$ .

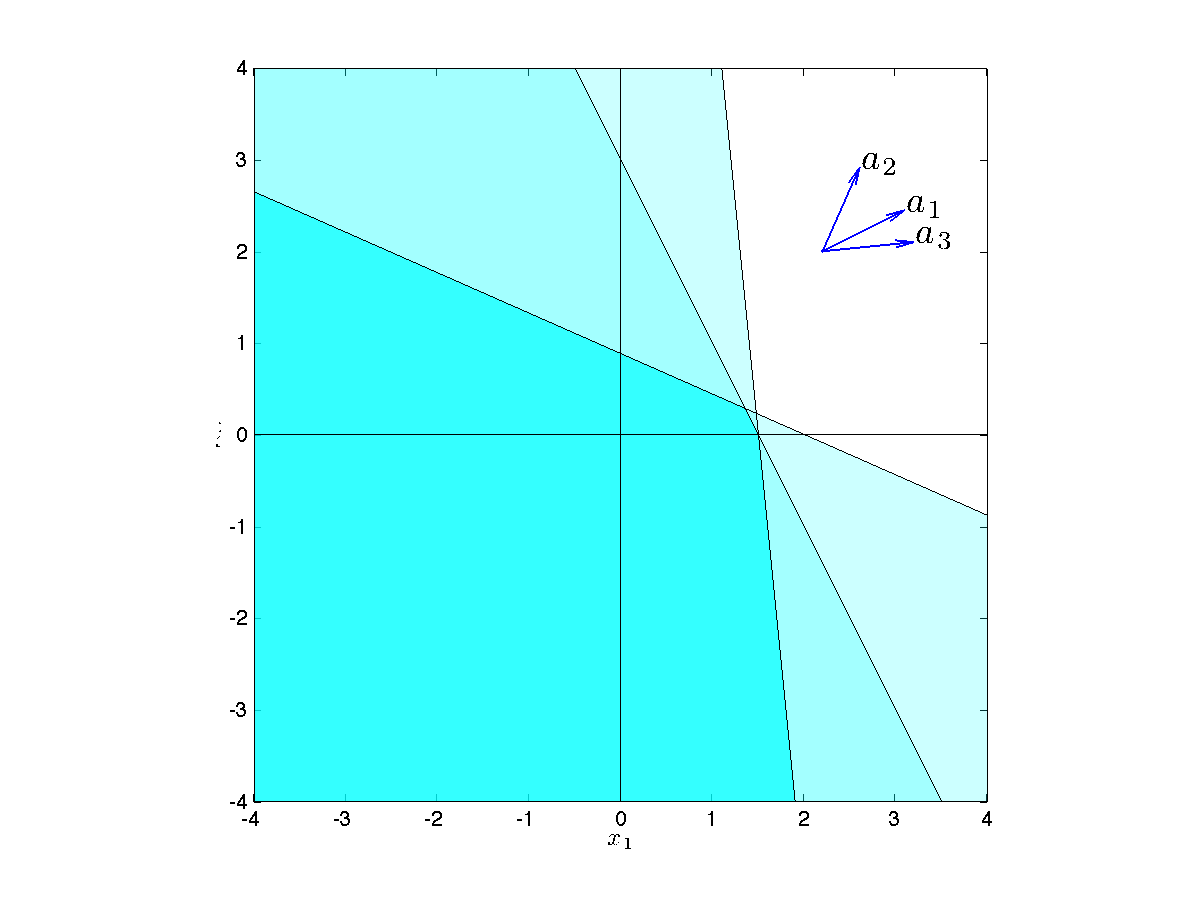
The scenario model is attractive for its simplicity. However, the number of scenarios can result in too large a problem.

A robust half-space constraint with scenario uncertainty, with three scenarios. The constraint represents a polyhedron (dark blue).

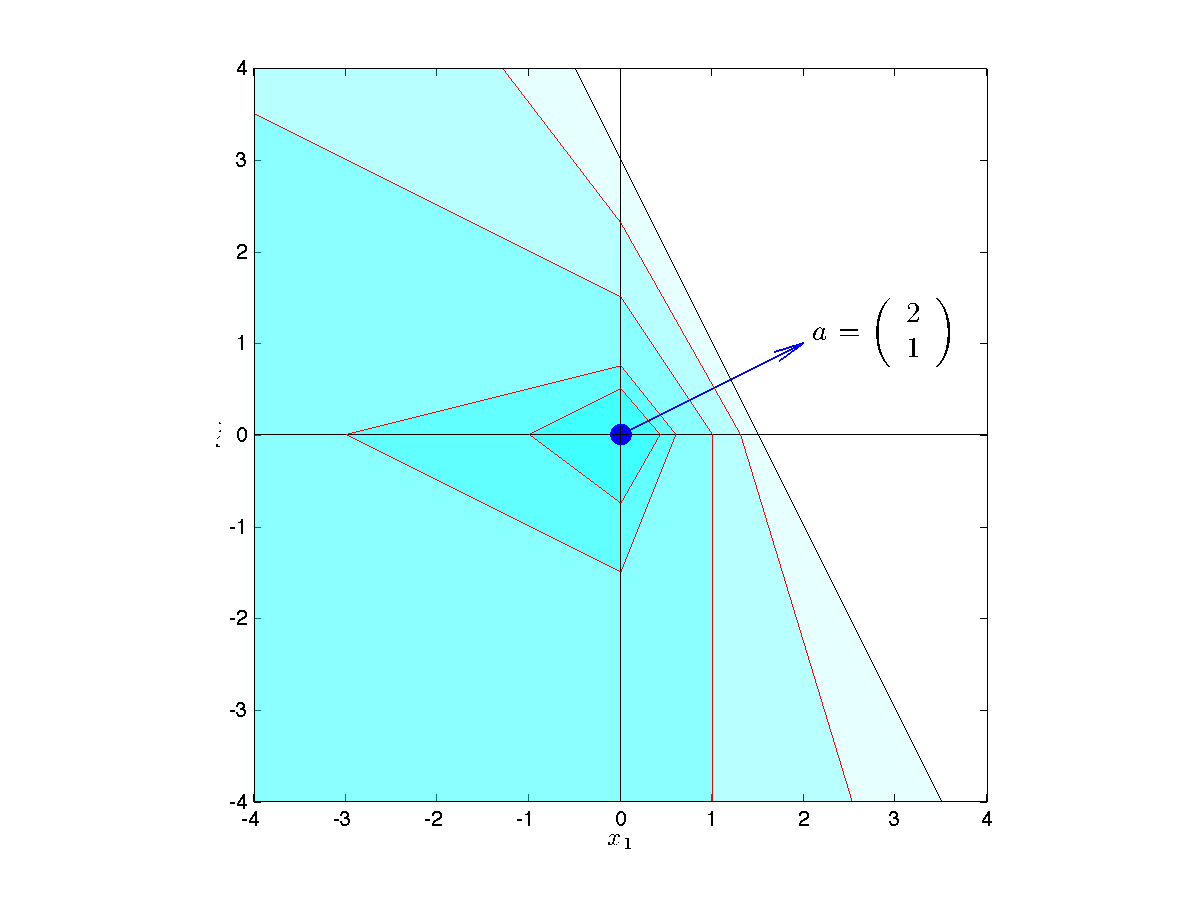
Example: Robust LP solution to the drug production problem.

Box uncertainty models

Definition

The box uncertainty model assumes that every coefficient vector 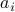a_i lies in a ‘‘box’’, or more generally, a hyper-rectangle in 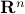$mathbf{R}^n$ , but is otherwise unknown. In its simplest case, the uncertainty model has the following form:

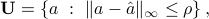
$mathbf{U} = left{ a ~:~ |a-hat{a}|_infty le rho right},$

where 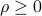rho ge 0 is a measure of the size of the uncertainty, and 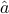hat{a} represents a ‘‘nominal’’ vector. This describes a ‘‘box’’ of half-diameter 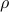rho around the center hat{a} .

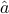Note that the robust counterpart to a half-space constraint

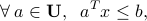
$forall : a in mathbf{U} , ;; a^Tx le b ,$

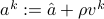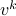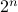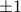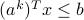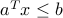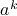can be handled as a scenario model, with “scenarios” the vectors $a^k := hat{a} + rho v^k$ , where v^k represents one of the 2^n vertices of the unit box (that is, vectors with pm 1 's as components). Indeed, enforcing the constraint (a^k)^Tx le b implies that a^Tx le b holds for every in the convex hull of the a^k 's, which is precisely the box 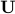mathbf{U} . This approach is not practical, as there are an exponential number of vertices, hence of constraints, to deal with.

Robust counterpart: LP formulation

The robust counterpart is better handled after one realizes that the robust counterpart constraint above is equivalent to

$b ge max_{a in mathbf{U}} : a^Tx .$

The maximization problem has a simple form (proof):

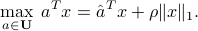
$max_{a in mathbf{U}} : a^Tx = hat{a}^Tx + rho |x|_1.$

A robust half-space constraint with box uncertainty, with different uncertainty levels. Such sets can be described by a finite (but exponential in the dimension) number of inequalities.

With a box uncertainty model, defined as 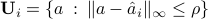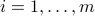$mathbf{U}_i = { a ::: |a-hat{a}_i|_infty le rho }$ , i=1,ldots,m , the robust counterpart to the original LP:

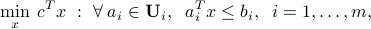
$min_x : c^Tx ~:~ forall : a_i in mathbf{U}_i , ;; a_i^Tx le b_i , ;; i= 1,ldots,m,$

is also an LP (in polyhedral form)

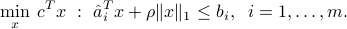
$min_x : c^Tx ~:~ hat{a}_i^Tx + rho |x|_1 le b_i , ;; i= 1,ldots,m.$

A robust LP with box uncertainty. The robust feasible set (darker blue) is inside the feasible set for the nominal LP (lighter blue); both feasible sets are polyhedral. The objective is to minimize c^Tx , where the vector is shown. The nominal LP has many optimal points (red line), which means a solution might be very sensitive to data changes (such as if we change the direction of the objective slightly). Although in this case, the roubst LP has a unique solution (red dot), it is still an LP, so it might be sensitive to changes in the objective vector.

Ellipsoidal uncertainty

Form of the model

The ellipsoidal uncertainty model has the form

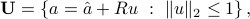
$mathbf{U} = left{ a = hat{a} + R u ~:~ |u|_2 le 1 right},$

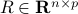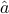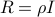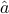where $R in mathbf{R}^{n times p}$ is a matrix which describes the “shape” of the ellipsoid around its center, which is hat{a} . If R = rho I for some rhoge 0 , then the above is a simple sphere of radius rho around hat{a} ; we refer to this special case as the spherical uncertainty model.

Ellipsoidal uncertainty models are useful to “couple” uncertainties across different components of the coefficient vector . This is contrast with the previous ‘‘box’’ models, which allow uncertainties to take their largest values independently of each other.

Robust counterpart: SOCP formulation

With an ellipsoidal model the robust counterpart is

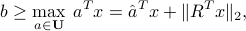
$b ge max_{a in mathbf{U}} : a^Tx = hat{a}^Tx + |R^Tx|_2,$

where we have exploited the Cauchy-Schwartz inequality. (See also here.)

A robust half-space constraint with spherical uncertainty, with different uncertainty levels.

With an ellipsoidal uncertainty model, defined as 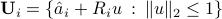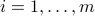$mathbf{U}_i = { hat{a}_i + R_i u ::: |u|_2 le 1 }$ , i=1,ldots,m , the robust counterpart to the original LP:

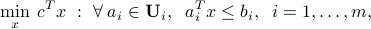
$min_x : c^Tx ~:~ forall : a_i in mathbf{U}_i , ;; a_i^Tx le b_i , ;; i= 1,ldots,m,$

becomes an SOCP:

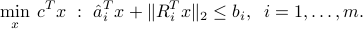
$min_x : c^Tx ~:~ hat{a}_i^Tx + |R_i^Tx|_2 le b_i , ;; i= 1,ldots,m.$

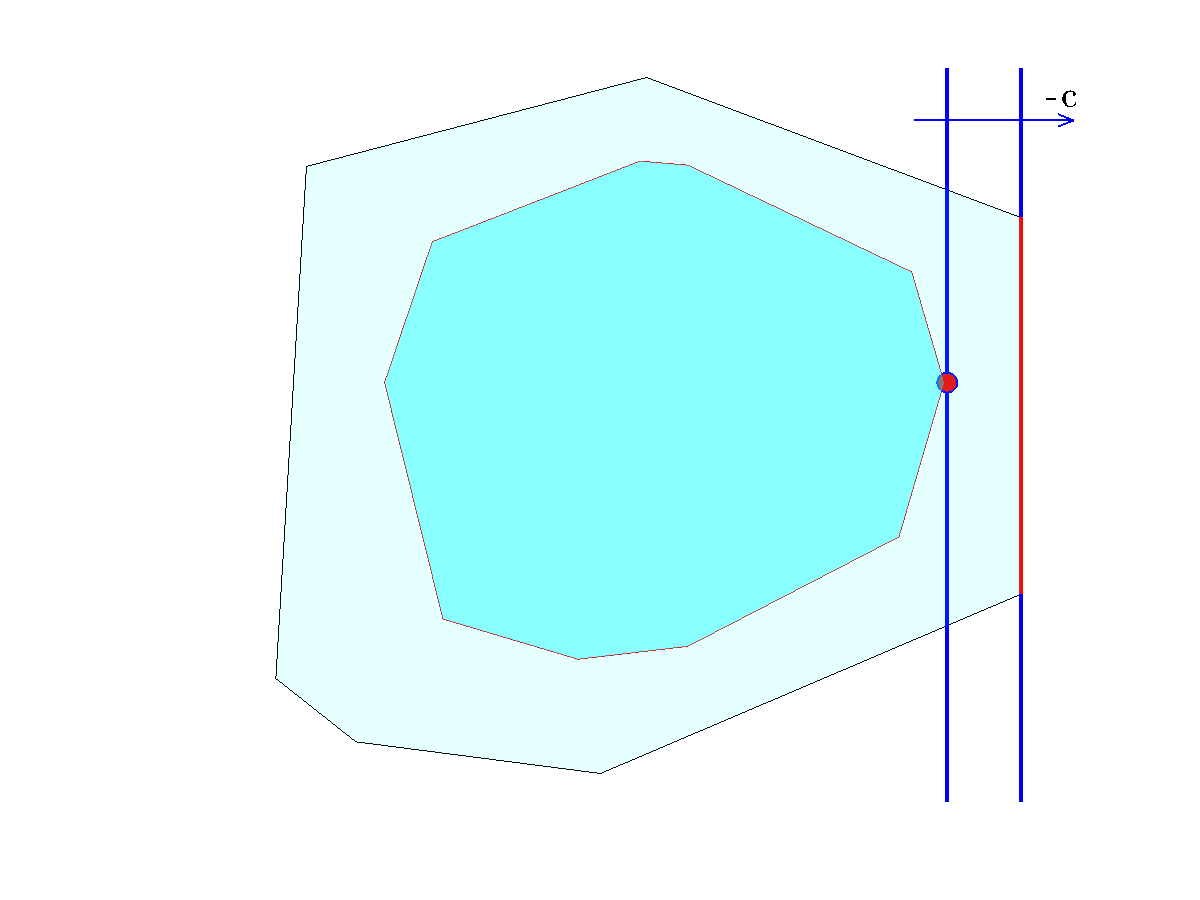
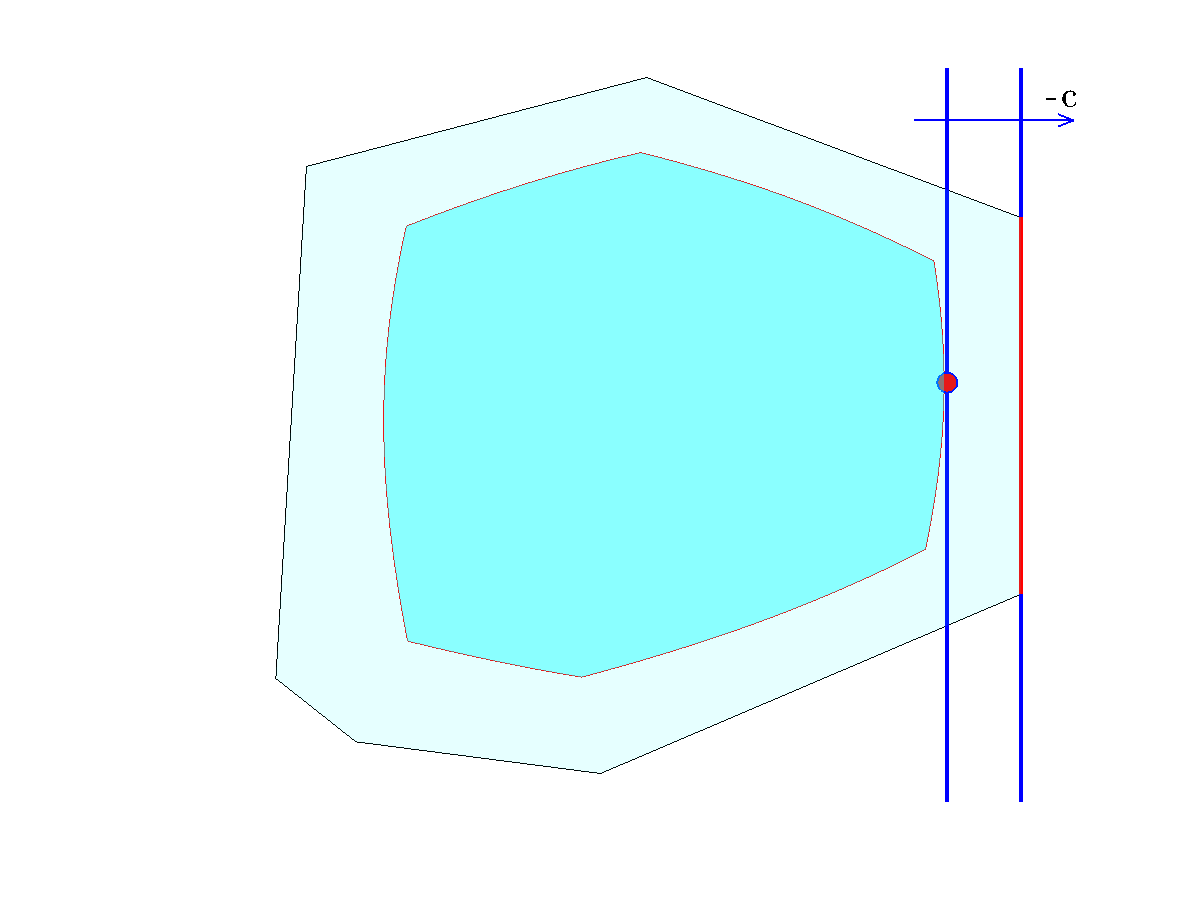
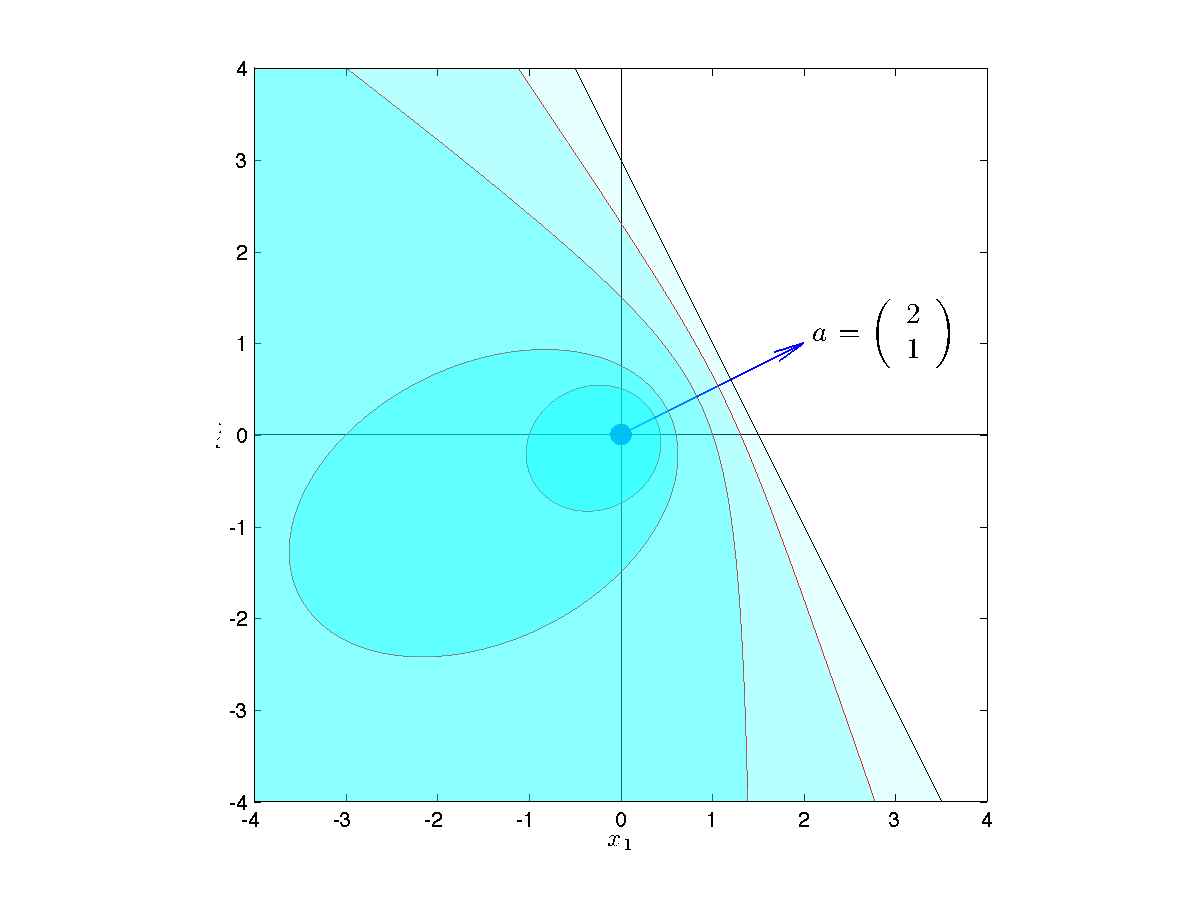
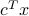A robust LP with spherical uncertainty. The robust feasible set (darker blue) is inside the (polyhedral) feasible set for the nominal LP (lighter blue). The objective is to minimize c^Tx , where the vector 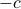is shown. The nominal LP has many optimal points (red line), which means a solution might be very sensitive to data changes (such as if we change the direction of the objective slightly). In constrast, the solution to the robust LP is unique (red dot), irrespective of the choice of the objective. As a result, it not very sensitive to changes in the objective or other problem data.