Optimization Models
Home
Software
Links
Index
Contact
1. Introduction
1.1. Overview
1.2. Optimization Models
2. Linear Algebra
2.1. Vectors
2.2. Matrices
2.3. Linear Equations
2.4.  Least-Squares
2.5. Eigenvalues
2.6  Singular Values
3. Convex Models
3.1. Convexity
3.2. LP and QP
3.3. SOCP
3.4. Robust LP
3.5. GP
3.6. SDP
3.7. Non-Convex Models
4. Duality
4.1. Weak Duality
4.2. Strong Duality
4.3.  Applications
5. Case Studies
5.1. Senate Voting
5.2. Antenna Arrays
5.3. Localization
5.4. Circuit Design

Optimality Conditions

  • Dual optimum attainment

  • Primal optimum attainment

  • Optimality conditions

  • Special cases

Sufficient condition for dual optimum attainment

Slater condition, namely strict feasibility of the primal, ensures that the dual problem is attained.

Primal optimum attainment

Likewise, if in addition the dual problem is strictly feasible, that is if:

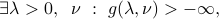
exists lambda >0 , ;; nu ~:~ g(lambda,nu) > -infty,

then strong duality holds, and both problems are attained, that is: there exist 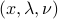(x,lambda,nu) such that

  • x is feasible for the primal problem;

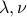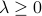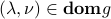  • lambda,nu are feasible for the dual problem: lambda ge 0, and (lambda,nu) in mbox{bf dom}g.

Example:

Complementary slackness

Assume that strong duality holds, and both primal and dual problems are attained, by 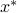x^ast and (lambda^ast,nu^ast) respectively. Then we have

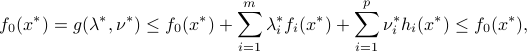
f_0(x^ast) = g(lambda^ast,nu^ast) le f_0(x^ast) + sum_{i=1}^m lambda_i^ast f_i(x^ast) + sum_{i=1}^p nu^ast_i h_i(x^ast) le f_0(x^ast),

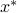where the first inequality is by definition of the dual function as a minimum over x, and the second from the fact that x^ast is feasible. Hence the sum in the above is zero. Since every term in that sum is non-positive, each term is zero:

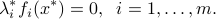
lambda_i^ast f_i(x^ast) = 0, ;; i=1,ldots,m.

The above are called the complementary slackness conditions. They imply that if the 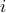i-th constraint is strictly satisfied, then the corresponding dual variable is zero. Conversely, if 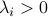lambda_i>0 then we must have f_i(x) = 0.

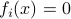Optimality conditions

The following conditions:

  • Primal feasibility:

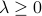
  • Dual feasibility: lambda ge 0

  • Lagrangian stationarity: (in the case when every function involved is differentiable)

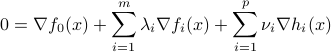
0 = nabla f_0(x) + sum_{i=1}^m lambda_i nabla f_i(x) + sum_{i=1}^p nu_i nabla h_i(x)

  • Complementary slackness are called the Karush-Kuhn-Tucker (KKT) conditions.

If the problem is convex, and satisfies Slater's condition, then a primal point is optimal if and only if there exist 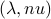(lambda,nu) such that the KKT conditions are satisfied. Conversely, the above conditions guarantee that strong duality holds, and 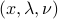(x,lambda,nu) are optimal.