Optimization Models
Home
Software
Links
Index
Contact
1. Introduction
1.1. Overview
1.2. Optimization Models
2. Linear Algebra
2.1. Vectors
2.2. Matrices
2.3. Linear Equations
2.4.  Least-Squares
2.5. Eigenvalues
2.6  Singular Values
3. Convex Models
3.1. Convexity
3.2. LP and QP
3.3. SOCP
3.4. Robust LP
3.5. GP
3.6. SDP
3.7. Non-Convex Models
4. Duality
4.1. Weak Duality
4.2. Strong Duality
4.3.  Applications
5. Case Studies
5.1. Senate Voting
5.2. Antenna Arrays
5.3. Localization
5.4. Circuit Design

Slater Condition for Strong Duality

  • Primal and dual problem

  • Strong duality

  • Slater's theorem

  • Geometry

Primal and Dual Problems

We consider a convex constrained optimization problem in standard form:

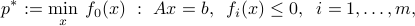
p^ast := min_x : f_0(x) ~:~ Ax = b, ;; f_i(x) le 0, ;; i=1,ldots, m,

where 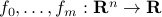f_0,ldots,f_m : mathbf{R}^n rightarrow mathbf{R} are convex functions, 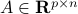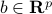A in mathbf{R}^{p times n}, b in mathbf{R}^p define the affine inequality constraints.

To this problem we associate the Lagrangian, wich is the function 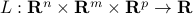L : mathbf{R}^n times mathbf{R}^m times mathbf{R}^{p} rightarrow mathbf{R} with values

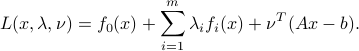
L(x,lambda,nu) = f_0(x) + sum_{i=1}^m lambda_i f_i(x) + nu^T(Ax-b).

The corresponding dual function is the function 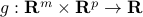g : mathbf{R}^m times mathbf{R}^{p} rightarrow mathbf{R} with values

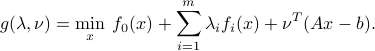
g(lambda,nu) = min_x : f_0(x) + sum_{i=1}^m lambda_i f_i(x) + nu^T(Ax-b).

Recall that the function 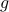g is concave, and that it can assume 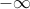-infty values. Its domain is

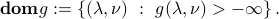
mbox{bf dom} g := left{ (lambda, nu) ~:~ g(lambda,nu) > -infty right}.

Finally, the dual problem reads

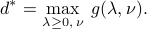
d^ast = max_{lambda ge 0, : nu} : g(lambda,nu).

Note that the sign constraints are imposed only on the dual variables corresponding to inequality constraints. Note also that there are (possibly) implicit constraints in the above problem, since we must have 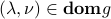(lambda,nu) in mbox{bf dom}g.

Strong duality

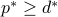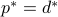The theory of weak duality seen here states that p^ast ge d^ast. This is true always, even if the original problem is not convex. We say that strong duality holds if p^ast = d^ast.

Slater's sufficient condition for strong duality

Slater's theorem provides a sufficient condition for strong duality to hold. Namely, if

  • The primal problem is convex;

  • It is strictly feasible, that is, there exists 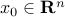x_0 in mathbf{R}^n such that

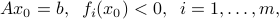
Ax_0 = b, ;; f_i(x_0) < 0, ;; i=1,ldots,m,

then, strong duality holds: 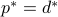p^ast = d^ast, and the dual problem is attained. (Proof)

Example:

Geometry

The geometric interpretation of weak duality shows why strong duality holds for a convex, strictly feasible problem. For simplicity again, we consider the case with no equality constraints, and a single convex constraint.

Recall that we can express the primal problem with two new scalar variables 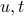u,t, as follows:

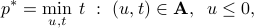
p^ast = displaystylemin_{u,t} : t ~:~ (u,t) in mathbf{A}, ;; u le 0,

where

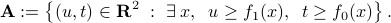
mathbf{A} := left{ (u,t) in mathbf{R}^2 ~:~ exists : x , ;; u ge f_1(x), ;; t ge f_0(x) right}.

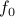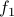Since the primal problem is convex, that is, f_0 and f_1 are convex functions, the above set is convex.

Strict primal feasibility means that the set 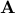mathbf{A} cuts ‘‘inside’’ the right-half of the 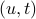(u,t)-plane. If that property holds, then we can attain the optimal point 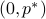(0,p^ast) by a tangent with a finite strictly negative slope. One implication is that 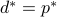d^ast = p^ast, that is, strong duality holds. This slope is precisely the optimal dual variable, 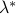lambda^ast; thus the dual problm is attained.