SOCPs include QCQps as a Special Case
Theorem: QCQPs as SOCPs
The quadratically constrained quadratic programming problem
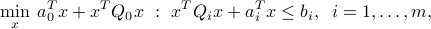
where  ,
, 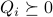 ,
,  , can be expressed as an SOCP with rotated second-order cone constraints:
, can be expressed as an SOCP with rotated second-order cone constraints:
![displaystylemin_{x,t,w_0,ldots,w_m} : a_0^Tx + t ~:~ begin{array}[t]{l} (w_0,t,1) in mathbf{K}_n, ;; w_0 = Q_0^{1/2}x, (w_i,b_i-a_i^Tx,1) in mathbf{K}_n , ;; w_i = Q_i^{1/2} x_i, ;; i=1,ldots, m . end{array}](eqs/2842135880024111324-130.png)
Proof: We first represent the problem in epigraph form:

Now, a constraint of the form

is equivalent to the existence of 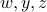 such that
such that

where 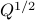 is the square-root of the PSD matrix
is the square-root of the PSD matrix 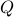 .
.
Applyng this to the constraints of the above formulation, we obtain an equivalent representation of the original QCQP:
![displaystylemin_{x,t} : a_0^Tx + t ~:~ begin{array}[t]{l} w_0^Tw_0 le t, ;; w_0 = Q^{1/2}x, w_i^Tw_i le b_i-a_i^Tx, ;; w_i = Q_i^{1/2} x_i, ;; i=1,ldots, m . end{array}](eqs/6054448220096727951-130.png)
The above can be written as given in the theorem, as claimed.