Second-Order Cone Optimization
Definitions
Examples
Definitions
Standard form
We say that a problem is a second-order cone optimization problem (SOCP) if it is a tractable conic optimization problem of the form (ref{eq:conic-pb-def-L6}), where the cone 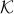 is a product of second-order cones and possibly the non-negative orthant
is a product of second-order cones and possibly the non-negative orthant 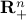 .
.
A standard form for the SOCP model is
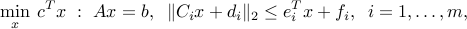
where we see that the variables 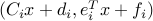 should belong to a second-order cone of appropriate size. This corresponds to a convex problem in standard form, with the constraint functions
should belong to a second-order cone of appropriate size. This corresponds to a convex problem in standard form, with the constraint functions 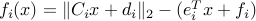 .
.
SOCPs contain LPs as special cases, as seen from the standard form above, with 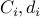 all zero.
all zero.
Special case: convex quadratic optimization
Convex quadratic optimization (often written QP for short) corresponds to the convex optimization model
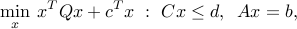
where 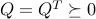 . Thus, QPs are extensions of LPs where a convex, quadratic term is added to the linear objective.
. Thus, QPs are extensions of LPs where a convex, quadratic term is added to the linear objective.
We can view QPs as special cases of SOCP: first, we express the problem in a way to make the objective linear:
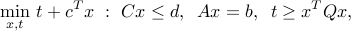
then we observe that the last constraint can be expressed using a rotated second-order cone. Precisely, we have 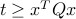 if and only if
if and only if 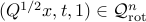 .
.
Quadratically constrained, convex quadratic optimization
QCQPs, as they are know by their acronym, correspond to problems of the form
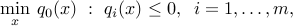
where the functions 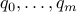 are all convex and quadratic:
are all convex and quadratic:
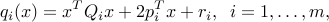
with 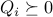 . Using rotated second-order cones, we can cast such problems as SOCPs.
. Using rotated second-order cones, we can cast such problems as SOCPs.
Note that SOCPs cannot, in general, be cast as QCQPs. Consider a single SOC constraint of the form
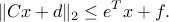
One may be tempted to square the SCO constraints and obtain a quadratic constraint of the form
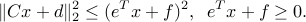
While the above constraints are equivalent to the original SOC constraint, the first is not convex.
Examples
Risk-return trade-off in portfolio optimizatio
Consider the problem of investing in 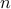 assets, whose returns over one period (say, a month) are described as a random variable
assets, whose returns over one period (say, a month) are described as a random variable 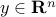 , with mean
, with mean 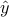 and covariance matrix
and covariance matrix 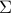 . A portfolio is described as a vector
. A portfolio is described as a vector 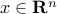 , with
, with 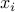 the amount invested in asset
the amount invested in asset 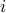 (if no short-selling is allowed, we impose
(if no short-selling is allowed, we impose 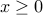 ; in general, we might impose that the portfolio vector belongs to a given polyhedron
; in general, we might impose that the portfolio vector belongs to a given polyhedron 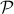 ). The return of the portfolio is then
). The return of the portfolio is then 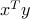 , and is a random variable with mean
, and is a random variable with mean 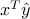 and variance
and variance 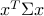 . The problem introduced by Markowitz seeks to find a trade-off between the expected return and the risk (variance) of the portfolio:
. The problem introduced by Markowitz seeks to find a trade-off between the expected return and the risk (variance) of the portfolio:
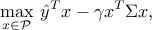
where 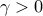 is a ‘‘risk-aversion’’ parameter. The above is a QP (convex quadratic program), a special case of SOCP.
is a ‘‘risk-aversion’’ parameter. The above is a QP (convex quadratic program), a special case of SOCP.
Robust half-space constraint
Consider a constraint on 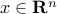 of the form
of the form 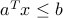 , with
, with 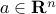 and
and 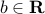 . Now assume that
. Now assume that  is only known to belong to an ellipsoid
is only known to belong to an ellipsoid 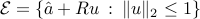 , with center
, with center 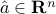 and
and 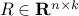 given. How can we guarantee that, irrespective of the choice of
given. How can we guarantee that, irrespective of the choice of 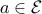 , we still have
, we still have 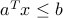 ?
?
The answer to this question hinges on the condition
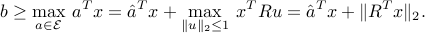
The above constraint is a second-order cone constraint.
Robust linear programming
Consider a linear optimization problem of the form
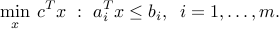
In practice, the coefficient vectors 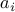 may not be known perfectly, as they are subject to noise. Assume that we only know that
may not be known perfectly, as they are subject to noise. Assume that we only know that 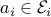 , where
, where 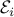 are given ellipsoids. In robust optimization, we seek to minimize the original objective, but we insist that each constraint be satisfied, irrespective of the choice of the corresponding vector
are given ellipsoids. In robust optimization, we seek to minimize the original objective, but we insist that each constraint be satisfied, irrespective of the choice of the corresponding vector 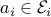 . Based on the earlier result, we obtain the second-order cone optimization problem
. Based on the earlier result, we obtain the second-order cone optimization problem
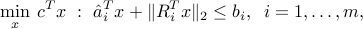
where 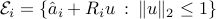 . In the above, we observe that the feasible set is smaller than the original one, due to the terms involving the
. In the above, we observe that the feasible set is smaller than the original one, due to the terms involving the 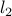 -norms.
-norms.
The figure above illustrates the kind of feasible set one obtains in a particular instance of the above problem, with spherical uncertainties (that is, all the ellipsoids are spheres, 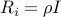 for some
for some 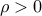 ). We observe that the robust feasible set is indeed contained in the original polyhedron.
). We observe that the robust feasible set is indeed contained in the original polyhedron.
Robust separation
We have discussed the problem of linear separation of two classes of points here. We revisit this example, assuming now that each point 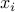 ,
, 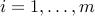 , is only known to belong to an ellipsoid
, is only known to belong to an ellipsoid 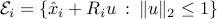 , where
, where 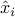 is the ‘‘nominal’’ value, and matrix
is the ‘‘nominal’’ value, and matrix 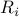 describes the ellipsoidal uncertainty around it. The condition for an hyperplane
describes the ellipsoidal uncertainty around it. The condition for an hyperplane 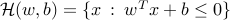 , where
, where 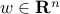 ,
, 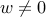 , and
, and 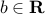 , to separate the ellipsoids is
, to separate the ellipsoids is
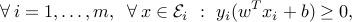
which is equivalent to the second-order cone constraints
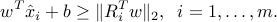
begin{figure}t
begin{center}
includegraphics= 00, height = 2.7in, width=3.5in{Figures/robl2svm.pdf}
caption{label{fig:rob-sphere-svm-L6}
A linear classifier that separates data points with maximal spherical uncertainty around them.}
end{center}
end{figure}
Consider the special case when all the ellipsoids are spheres of given radius 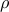 , that is,
, that is, 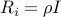 ,
, 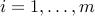 . Now look for the hyperplane that is maximally robust, that is, tolerates the largest amount of uncertainty in the data points (as measured by
. Now look for the hyperplane that is maximally robust, that is, tolerates the largest amount of uncertainty in the data points (as measured by 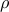 ). Our problem writes
). Our problem writes
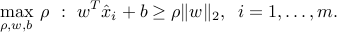
Since the constraints are homogeneous in  , we can without loss of generality impose
, we can without loss of generality impose 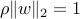 . We then formulate the above problem as the LP
. We then formulate the above problem as the LP
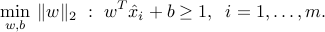
The quantity 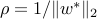 is called the margin of the optimal classifier, and gives the largest amount of spherical uncertainty the data points can tolerate before they become not separable.
is called the margin of the optimal classifier, and gives the largest amount of spherical uncertainty the data points can tolerate before they become not separable.