Convex Sets

Convexity > Convex Sets | Convex Functions | Convex Problems | Simple Algorithm

Definition
Operations that preserve convexity
Separation theorems

Definition

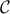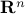A subset {cal C} of $mathbf{R}^n$ is convex if and only if it contains the line segment between any two points in it:
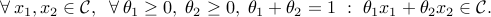
$forall : x_1, x_2 in {cal C}, ;; forall : theta_1 ge 0, ; theta_2 ge 0, ; theta_1 + theta_2 = 1 ~:~ theta_1 x_1 + theta_2 x_2 in {cal C}.$
Some important special cases of convex sets are the following.

The set is said to be an affine subspace if it contains the entire line passing through any two points. This corresponds to the condition above, with 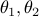arbitrary. Subspaces and affine subspaces are convex.

The set is said to be a convex cone if the condition above holds, but with the restriction 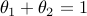removed.

Examples:

The convex hull of a set of points 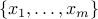${ x_1,ldots,x_m}$ is defined as
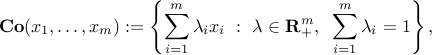
$mbox{bf Co} (x_1,ldots,x_m) := left{ sum_{i=1}^m lambda_i x_i ~:~ lambda in mathbf{R}^m_+, ;; sum_{i=1}^m lambda_i = 1 right},$
and is convex. The conic hull:
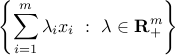
$left{ sum_{i=1}^m lambda_i x_i ~:~ lambda in mathbf{R}^m_+ right}$
is a convex cone.

For 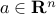$a in mathbf{R}^n$ , and 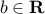, the hyperplane 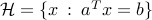${cal H} = { x ::: a^Tx = b }$ is affine. The half-space 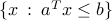${ x ::: a^Tx le b }$ is convex.

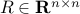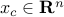For a square, non-singular matrix $R in mathbf{R}^{n times n}$ , and $x_c in mathbf{R}^n$ , the ellipsoid 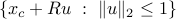${ x_c + Ru ~:~ |u|_2 le 1 }$ is convex. (The center of the epllipsoid is 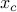, and you can think of 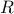as the “radius”.) With 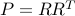, we can describe the ellipsoid as
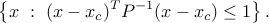
$left{ x ~:~ (x-x_c)^TP^{-1} (x-x_c) le 1 right}.$

A polyhedron is a set described by a finite number of affine inequalities and equalities: (

{cal P} = left{ x : Ax le b, ;; Cx = d right}, ) where A,C are matrices, 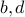b,d are vectors, and inequalities are understood component-wise. Sometimes bounded polyhedra are referred to as polytopes. As a specific example, the probability simplex
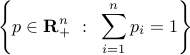
$left{ p in mathbf{R}^n_+ ~:~ sum_{i=1}^n p_i = 1 right}$
is a special case of a polyhedron, and is useful to describe discrete probabilities.

The second-order cone
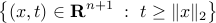
$left{ (x,t) in mathbf{R}^{n+1} ~:~ t ge |x|_2 right}$
is a convex cone. It is sometimes called ‘‘ice-cream cone’’, for obvious reasons. (We will prove the convexity of this set later.)

The positive semi-definite cone (

{cal S}_+^n := left{ X = X^T in mathbf{R}^{n times n} : X succeq 0 right} ) is a convex cone. (Again, we will prove the convexity of this set later.)

Operations that preserve convexity

Two important operations that preserve convexity are:

Intersection: the intersection of a (possibly infinite) family of convex sets is convex. We can use this property to prove that the semi-definite cone 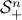${cal S}_+^n$ is convex, since (

{cal S}_+^n = left{ X =X^T in mathbf{R}^{n times n} : forall : z in mathbf{R}^n, ;; z^TXz ge 0 right}, ) from which we see that the set is the intersection of the subspace of symmetric matrices with a set described by an infinite number of linear inequalities of the form 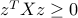, indexed by 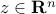$z in mathbf{R}^n$ . 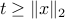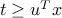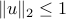Likewise, the second-order cone defined in (ref{eq:soc-def-L3}) is convex, since the condition t ge |x|_2 is equivalent to the infinite number of affine inequalities t ge u^Tx , |u|_2le 1 .

Affine transformation: If a function is affine (that is, it is the sum of a linear function and a constant), and 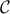is convex, then the set

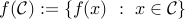
is convex. A particular example is projection on a subspace, which preserves convexity.

Separation theorems

There are many versions of separation theorems in convex analysis. One of them is the separating hyperplane theorem:

Theorem: Separating hyperplane

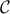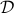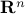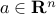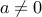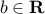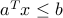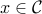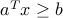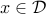If {cal C} , {cal D} are two convex subsets of $mathbf{R}^n$ that do not intersect, then there is an hyperplane that separates them, that is, there exit $a in mathbf{R}^n$ , a ne 0 , and b in mathbf{R} , such that a^Tx le b for every x in {cal C} , and a^Tx ge b for every x in {cal D} .

Another result involves the separation of a set from a point on its boundary:

Theorem: Supporting hyperplane

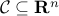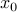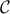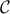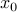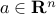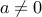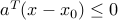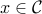If ${cal C} subseteq mathbf{R}^n$ is convex and non-empty, then for any x_0 at the boundary of {cal C} , there exist a supporting hyperplane to {cal C} at x_0 , meaning that there exist $a in mathbf{R}^n$ , a ne 0 , such that a^T(x-x_0) le 0 for every x in {cal C} .