Outer Spherical Approximations
Outer spherical approximation via gridding
Outer spherical approximation via Lagrange relaxation
Improved spherical approximation via affine Lagrange multipliers
Let us consider a candidate sphere 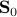 , of center
, of center 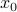 and radius
and radius 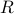 . We formulate the condition that the sphere
. We formulate the condition that the sphere 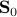 contains the intersection of all the spheres of center
contains the intersection of all the spheres of center 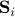 , as follows:
, as follows:
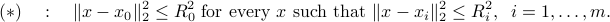
This conditions appears to be hard to check.
Outer spherical approximation via gridding
A first approach, which works well only in moderate dimensions (2D or 3D), simply entails gridding the boundary of the intersection. In 2D, we can parametrize the boundary explicitly, as a curve, using an angular parameter. For each angular direction ![theta in [0,2pi]](eqs/1626472798141214711-130.png) , we can easily find the point that is located on the boundary of the intersection, in the direction given by
, we can easily find the point that is located on the boundary of the intersection, in the direction given by  : we simply maximize
: we simply maximize  such that the point
such that the point  is inside everyone of the spheres. (There is an explicit formula for the maximal value.)
is inside everyone of the spheres. (There is an explicit formula for the maximal value.)
One we have computed 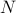 points on the boundary,
points on the boundary, 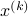 ,
, 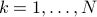 , we simply solve the SOCP
, we simply solve the SOCP
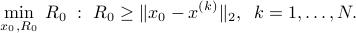
The gridding approach suffers from the fact that we need to grid finely to be able to guarantee that the spherical approximation we are computed indeed contains all the points on the intersection. On the other hand, too fine a grid results in a large number of constraints, which in turn adversely impacts the time needed to solve the above problem.
Outer spherical approximation via Lagrange duality
We now develop an alternate approach which relies on weak duality concepts.
A sufficient condition
A sufficient condition for the above condition 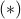 to hold is that there exist a non-negative vector
to hold is that there exist a non-negative vector  such that
such that
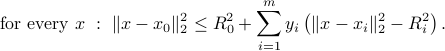
Indeed, it is easily checked that if a point  belongs to all the spheres, then indeed the sum above is less or equal than
belongs to all the spheres, then indeed the sum above is less or equal than 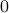 when
when 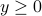 .
.
Minimizing the radius 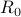 subject to the condition that the above holds for some
subject to the condition that the above holds for some 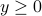 will result in a conservative (larger) estimate of the amount of uncertainty.
will result in a conservative (larger) estimate of the amount of uncertainty.
SOCP formulation
Alternatively we can express the above condition as:
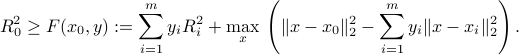
The problem of minimizing the radius 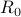 subject to the above condition can thus be written as
subject to the above condition can thus be written as
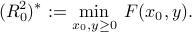
It turns out that we can express the function 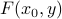 in closed-form, as proven here:
in closed-form, as proven here:
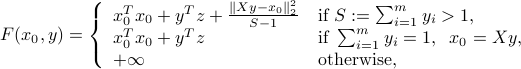
where for notational convenience we use the matrix 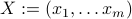 and the vector
and the vector  with components
with components 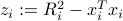 ,
, 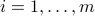 . (Remember that our measurement consistency condition holds, so that
. (Remember that our measurement consistency condition holds, so that 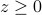 .)
.)
We are led to consider the sub-problem of minimizing 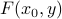 over
over 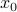 , with
, with 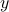 fixed. If
fixed. If 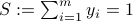 , then we must have
, then we must have 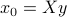 . If
. If 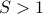 ,
, 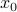 must solve
must solve
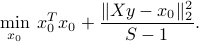
Again, this a convex quadratic problem, with a (unique) solution obtained by taking derivatives. A minimizer is 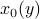 , where
, where
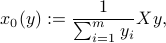
that is, 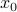 is the weighted average, with weights given by
is the weighted average, with weights given by 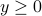 , of the points
, of the points 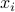 . Note that the expression remains valid when
. Note that the expression remains valid when 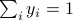 , since then we must have
, since then we must have 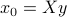 .
.
Plugging the above value of 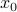 in the problem leads to a problem in variable
in the problem leads to a problem in variable 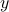 only:
only:
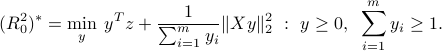
The above problem can be solved as an SOCP with rotated second-order cone constraints:
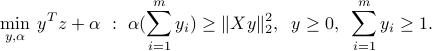
A simpler formulation (consistent measurements)
We can obtain a simpler formulation that involves QP only. We now use our measurement consistency assumption, which translates as 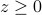 . First we replace the variable
. First we replace the variable 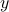 with two new variables
with two new variables 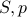 , and a new constraint. The new variables
, and a new constraint. The new variables 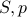 are defined as
are defined as
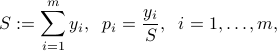
and the new constraint is 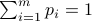 . We obtain the new problem
. We obtain the new problem
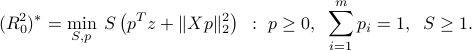
Since 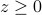 , the term inside the parentheses is non-negative, and thus
, the term inside the parentheses is non-negative, and thus 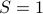 is optimal. Hence the problem reduces to a QP:
is optimal. Hence the problem reduces to a QP:
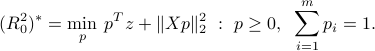
This provides the optimal radius. The optimal point is
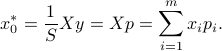
An improved condition via affine duality
To improve our condition, we start from the equivalent condition for intersection containment:
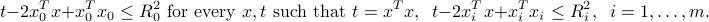
We now consider a relaxed of the form
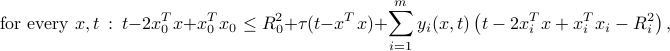
where 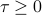 , and the
, and the 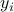 's are now non-negative functions of
's are now non-negative functions of 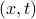 . (Before, we chose them to have constant values.) The above is still hard to check in general, but becomes easy if we make the assumption that the functions
. (Before, we chose them to have constant values.) The above is still hard to check in general, but becomes easy if we make the assumption that the functions 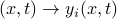 are affine.
are affine.
We proceed by taking the vector 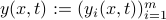 to be of the form
to be of the form
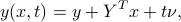
where 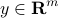 ,
, 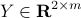 and
and 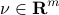 will be variables. (The case before will be recovered upon setting
will be variables. (The case before will be recovered upon setting 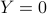 ,
, 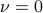 .)
.)
The condition above becomes a single quadratic condition on 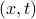 :
:
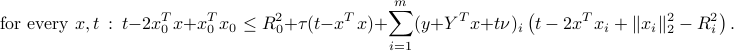
The above can be equivalently expressed as a positive semi-definiteness condition on a symmetric matrix that is affine in 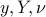 :
:
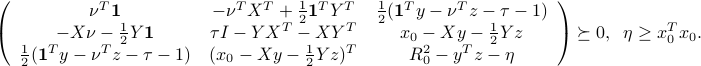
It remains to express the condition that the affine functions 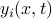 should be non-negative on the intersection. Precisely, we seek to enforce that for every
should be non-negative on the intersection. Precisely, we seek to enforce that for every 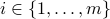 , the condition
, the condition

holds (here, 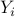 stands for the
stands for the 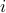 -th column of matrix
-th column of matrix 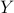 ). Now, we apply direct Lagrange duality. A sufficient condition for the above to hold is that there exist non-negative numbers
). Now, we apply direct Lagrange duality. A sufficient condition for the above to hold is that there exist non-negative numbers 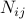 ,
, 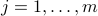 , such that
, such that
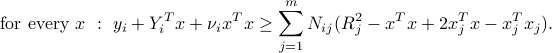
Again, the above is equivalent to a single linear matrix inequality in the variables 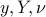 and
and 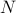 :
:
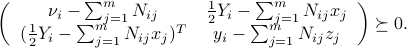
Putting this together, we obtain the SDP in variables 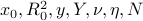 :
:
![min : R_0^2 ~:~ begin{array}[t]{l} left( begin{array}{ccc} nu^Tmathbf{1} & -nu^TX^T+frac{1}{2}mathbf{1}^TY^T & frac{1}{2}(mathbf{1}^Ty - nu^Tz -tau-1) -Xnu-frac{1}{2}Ymathbf{1} &tau I - YX^T-XY^T & x_0 - Xy - frac{1}{2}Yzfrac{1}{2}(mathbf{1}^Ty - nu^Tz -tau-1) & (x_0 - Xy - frac{1}{2}Yz)^T & R_0^2 - y^Tz-eta end{array}right) succeq 0, ;; eta ge x_0^Tx_0 left( begin{array}{cc} nu_i - sum_{j=1}^m N_{ij} & frac{1}{2} Y_i - sum_{j=1}^m N_{ij}x_j (frac{1}{2} Y_i - sum_{j=1}^m N_{ij}x_j)^T & y_i - sum_{j=1}^m N_{ij} z_j end{array}right) succeq 0, ;; i=1,ldots,m, end{array}](eqs/3393953924836324334-130.png)

 points on the boundary to enforce the constraint that the outer sphere contains the intersection. As a result, our approximation is not really an outer approximation, as it does not contain all the intersection points.
points on the boundary to enforce the constraint that the outer sphere contains the intersection. As a result, our approximation is not really an outer approximation, as it does not contain all the intersection points.

