From LP to Conic Optimization

SDP > Conic Problems | LMIs | Standard Forms | Applications

In the late 1980s, researchers were trying to generalize linear programming. At that time, LP was known to be solvable efficiently. Theory even showed that LPs could be solved in in time roughly cubic in the number of variables or constraints. The new interior-point methods for LP had just become available, and their excellent practical performance matched the theoretical complexity bounds. It seemed however that, beyond linear problems, one encountered a wall. Except for a few special problem classes, such as QP, it appeared that as soon as a problem contained non-linear terms, one would no hope the nice practical and theoretical efficiency allowed to LP.

In previous decades, it had been noted that convex problems could be efficiently solved in theory (under some mild conditions), however the known methods were extremely slow in practice. It seemed however that to harness the power of interior-point methods and apply it to problems other than LP, one had to look closely at convex optimization.

A breakthrough occurred by rethinking the role of the set of non-negative vectors, which is the basic object in LP. In a standard form, an LP can be written as

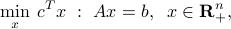
$min_x : c^Tx ~:~ Ax = b, ;; x in mathbf{R}_{+}^n,$

where 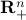$mathbf{R}_{+}^n$ is the set of non-negative vectors. Researchers asked: ‘‘what are the basic characteristics of $mathbf{R}_{+}^n$ that make interior-point methods work so well? In other words, are there other sets that could be used in place of $mathbf{R}_{+}^n$ , and still allow efficient methods"? It turns out that it is always possible to restrict attention to cones, that is, sets that are invariant by positive scaling of their elements.

At first glance, one can replace the set 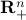$mathbf{R}_{+}^n$ by any convex cone, say mathbf{K} ; the new problem

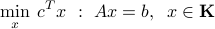
$min_x : c^Tx ~:~ Ax = b, ;; x in mathbf{K}$

is convex. But, as mentioned above, convexity alone is not sufficient to guarantee the existence of a practically efficient algorithm to solve it. It turns out that are a few convex cones mathbf{K} that are amenable to an efficient extension of interior-point methods.

One if the second-order cone, or any combination of second-order cones (arising when, say some variables are in a cone, others in another, and all are coupled by affine equalities). The SOCP class was the first beneficiary of the new class of algorithms.

Another class of problems involve the cone of positive semi-definite matrices, which leads to the class of semi-definite programs (SDP). SDPs involve a linear objective, matrix variables, and affine equality constraints, and positive semi-definiteness constraints on the (matrix) variables.

For both SOCP and SDP, the interior-point methods that work so well for LP can be extended. This comes of course at a price: the size of SOCPs that can be solved in reasonable time is smaller than for LP, and the complexity of SDPs is even higher. What we gain in the process is a much wider expressive power of the model.