Group sparsity and the 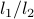-norm trick

SOCP > SOC inequalities | Standard forms | Group sparsity | Applications

Group sparsity problem
The 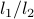-norm heuristic

Group sparsity problem

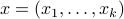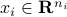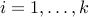In many applications, such as image annotation, we would like to encourage the occurrences of whole blocks of zeros in the decision vector. Assume for example that the decision vector is partitioned into two disjoint groups x = (x_1,ldots,x_k) , with $x_i in mathbf{R}^{n_i}$ , i=1,ldots,k , with 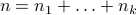n = n_1+ldots+n_k . We seek to minimize the number of non-zero blocks 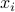x_i , while satisfying some constraint, say 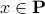x in mathbf{P} , with 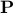a given polytope.

The 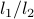-norm heuristic

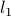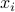We can use the l_1 -norm trick on the vector of Euclidean norms (|x_1|_2,ldots,|x_k|_2) . (This will encourage many of the blocks x_i to be zero; those blocks that are not zero will not, in general, be sparse.)

This leads to the problem

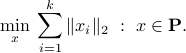
$min_x : sum_{i=1}^k |x_i|_2 ~:~ x in mathbf{P}.$

The above is a second-order cone program. This is easily seen after introducing a new vector variable

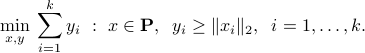
$min_{x,y} : sum_{i=1}^k y_i ~:~ x in mathbf{P}, ;; y_i ge |x_i|_2, ;; i=1,ldots,k.$

The following CVX snippets actually uses the above representation for the least-squares problem with a block-norm penalty:

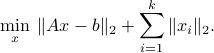
$min_x : |Ax-b|_2 + sum_{i=1}^k |x_i|_2.$

In our implementation we assume that each block 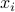x_i is of the same length .

CVX code

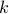cvx_begin variable x(n); variable y(k); minimize( norm(Ax-b,2) lambdasum( y ) ) subject to for i=1:k, y(i) >= norm(x((i-1)*p(1:p)),2); end cvx_end

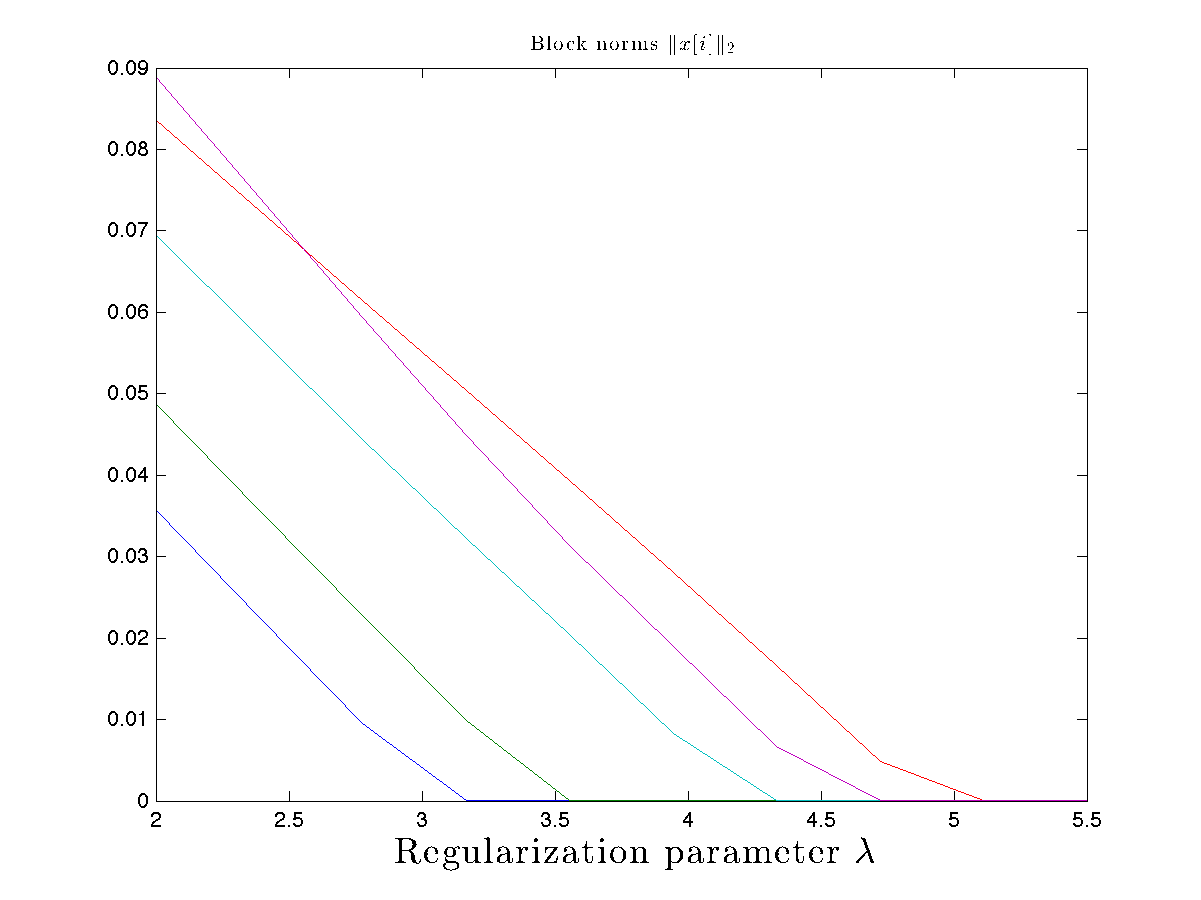In this example we