Cardinality minimization: the L1-norm trick
Cardinality mimimization problem
The
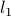 -norm heuristic
-norm heuristic Why does it work?
Application: piece-wise constant fitting
Cardinality Minimization
Many problems in engineering and scientific computing can be cast as
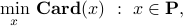
where 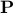 is a polyhedron (or, more generally, a convex set), and
is a polyhedron (or, more generally, a convex set), and 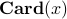 denotes the cardinality (number of non-zero elements) of the vector
denotes the cardinality (number of non-zero elements) of the vector  . Such problems seek a ‘‘sparse’’ solution, one with many zeroes in it.
. Such problems seek a ‘‘sparse’’ solution, one with many zeroes in it.
A related problem is a penalized version of the above, where we seek to trade-off an objective function against cardinality:
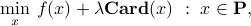
where  is some (usually convex) ‘‘cost’’ function, and
is some (usually convex) ‘‘cost’’ function, and 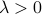 is a penalty parameter.
is a penalty parameter.
Cardinality minimization is a hard problem in general. It appears in many areas, such as classification.
The 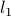 -norm heuristic
-norm heuristic
The 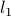 -norm heuristic consists in replacing the (non-convex) cardinality function
-norm heuristic consists in replacing the (non-convex) cardinality function 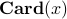 with a polyhedral (hence, convex) one, involving the
with a polyhedral (hence, convex) one, involving the 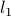 -norm. This heuristic leads to replace the problem at the top with
-norm. This heuristic leads to replace the problem at the top with
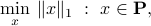
which is an LP (provided 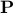 is a polyhedron).
is a polyhedron).
If 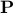 is described via affine inequalities, as
is described via affine inequalities, as 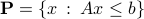 , with
, with  a matrix and
a matrix and 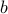 a vector existing in the matlab workspace, then the following CVX snippet solves the above problem.
a vector existing in the matlab workspace, then the following CVX snippet solves the above problem.
cvx_begin
variable x(n,1)
minimize( norm(x,1) )
subject to
Ax <= b;
cvx_end
Why does it work?
The 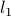 -norm heuristic often works well, especially if the variable
-norm heuristic often works well, especially if the variable  is bounded.
is bounded.
Often the variable is not bounded a priori, but its size is penalized, say by a squared 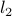 -norm. Consider an optimization problem of the form
-norm. Consider an optimization problem of the form
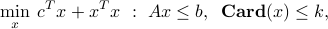
where 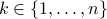 is a given integer that bounds the number of non-zeroes in the variable. Invoking the Cauchy-Schwartz inequality between
is a given integer that bounds the number of non-zeroes in the variable. Invoking the Cauchy-Schwartz inequality between  and the vector
and the vector 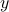 with
with  's where
's where  is non-zero, and
is non-zero, and 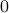 's elsewhere, we obtain (with
's elsewhere, we obtain (with 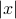 the vector with elements
the vector with elements 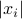 ,
, 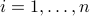 ):
):
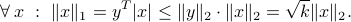
Hence, instead of solving the difficult problem above, we can solve for a lower bound:
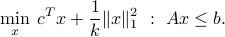
The above problem is convex. In fact, it can be written as the QP, by adding new variables:
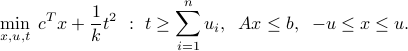
As often, CVX allows a direct implementation of the problem, but care must be taken to use the square_pos function to model the squared  -norm, as discussed in do's and don'ts of CVX.
-norm, as discussed in do's and don'ts of CVX.
cvx_begin
variable x(n)
minimize( c'*x + (1/k^2)*square_pos(norm(x,1)) )
cvx_end