Polyhedra
Half-spaces
Polyhedra
Half-spaces
Definition
A half-space is a set defined by a single affine inequality. Precisely, a half-space in 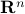 is a set of the form
is a set of the form
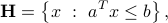
where 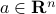 ,
, 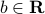 . A half-space is a convex set, the boundary of which is a hyperplane.
. A half-space is a convex set, the boundary of which is a hyperplane.
A half-space separates the whole space in two halves. The complement of the half-space is the open half-space 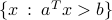 .
.
Geometry
A half-space separates the whole space in two halves. The complement of the half-space is the open half-space 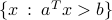 .
.
 |
When 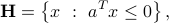
is the set of points which form an obtuse angle (between |
 |
When 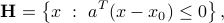
where |
Example: A half-space in 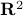 .
.
Link with linear functions
Hyperplanes correspond to level sets of linear functions.
Half-spaces represent sub-level sets of linear functions: the half-space above describes the set of points such that the linear function  achieves the value
achieves the value 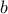 , or less. A quick way to check which half of the space the half-space describes is to look at where the origin is: if
, or less. A quick way to check which half of the space the half-space describes is to look at where the origin is: if 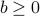 , then
, then  is in the half-space.
is in the half-space.
Polyhedra
Definition
A polyhedra is a set described finitely many affine inequalities. Precisely, a polyhedron is a set of the form
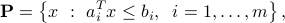
where 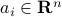 ,
, 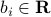 ,
,  .
.
A polyhedron can be expressed as the intersection of (finitely many) half-spaces:
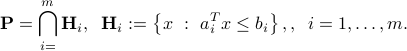
Geometry
A polyhedron is a convex set, with boundary made up of ‘‘flat’’ boundaries (the technical term is facet). Each facet corresponds to one of the hyperplanes defined by 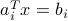 . The vectors
. The vectors 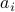 are orthogonals to the facets, and point outside the polyhedra.
are orthogonals to the facets, and point outside the polyhedra.
Note that not every set with flat boundaries can be represented as a polyhedron: the set has to be convex.
Matrix notation
It is often convenient to describe a half-space in matrix notation:
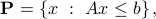
where 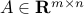 and
and 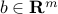 are defined as follows:
are defined as follows:
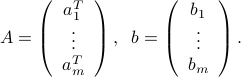
Here, we adopted the component-wise inequality convention: the notation 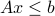 means that for every
means that for every  , the corresponding components of
, the corresponding components of 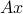 and
and 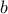 are ordered:
are ordered: 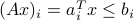 .
.
Example: A polyhedron in 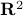 .
.
Equality constraints are allowed
Sets defined by affine inequalities and equalities are also polyhedra.
Indeed, consider the set
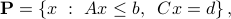
where 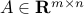 ,
, 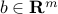 define the (component-wise) inequalities, and
define the (component-wise) inequalities, and 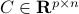 ,
, 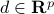 define the equalities.
define the equalities.
The set above can be expressed as an ‘‘inequalities-only’’ polyhedron:
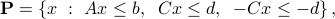
which can be put in the standard form for polyhedra, with augmented matrices and right-hand side vector.
Example: The probability simplex.
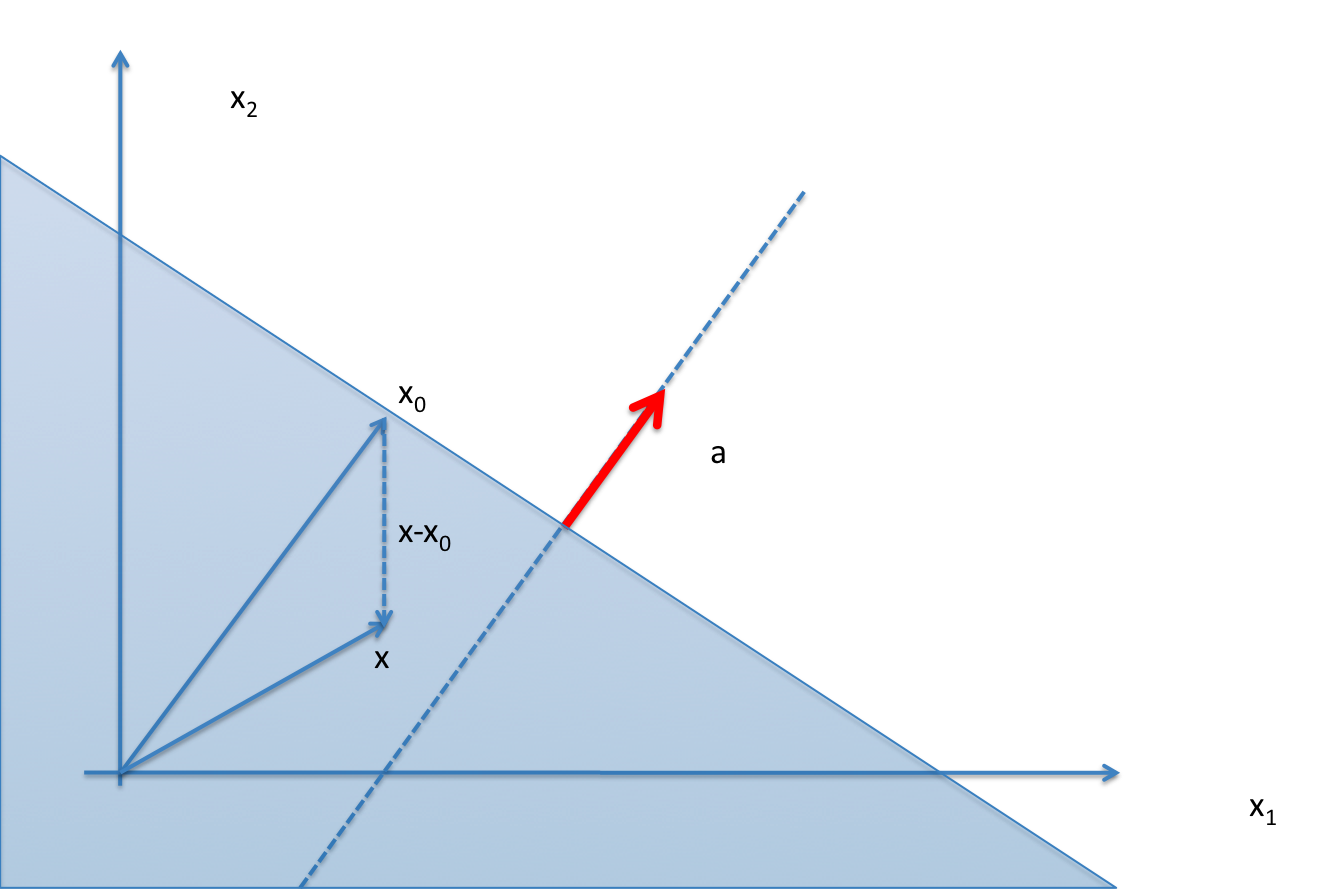
 , the half-space
, the half-space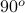 and
and 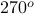 ) with the vector
) with the vector  . The boundary of this set is a subspace, the hyperplane of vectors orthogonal to
. The boundary of this set is a subspace, the hyperplane of vectors orthogonal to  , the half-space
, the half-space 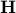 can be written as
can be written as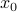 is chosen such that
is chosen such that 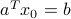 . For example,
. For example, 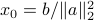 is such a point on the boundary of the half-space (this particular choice corresponds to the
is such a point on the boundary of the half-space (this particular choice corresponds to the 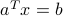 ). Thus, the half-space above corresponds to the set of points such that
). Thus, the half-space above corresponds to the set of points such that 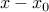 (shown in dotted) forms an obtuse angle with the vector
(shown in dotted) forms an obtuse angle with the vector