Hyperplanes
Hyperplanes
Projection on a hyperplane
Geometry
Half-spaces
Hyperplanes
A hyperplane is a set described by a single scalar product equality. Precisely, an hyperplane in 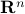 is a set of the form
is a set of the form
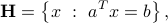
where 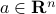 ,
, 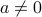 , and
, and 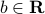 are given.
When
are given.
When  , the hyperplane is simply the set of points that are orthogonal to
, the hyperplane is simply the set of points that are orthogonal to  ; when
; when 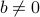 , the hyperplane is a translation, along direction
, the hyperplane is a translation, along direction  , of that set.
, of that set.
If 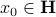 , then for any other element
, then for any other element 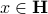 , we have
, we have
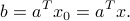
Hence, the hyperplane can be characterized as the set of vectors  such that
such that 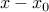 is orthogonal to
is orthogonal to  :
:
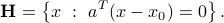
Hyperplanes are affine sets, of dimension  (see the proof here). Thus, they generalize the usual notion of a plane in
(see the proof here). Thus, they generalize the usual notion of a plane in  . Hyperplanes are very useful because they allows to separate the whole space in two regions. The notion of half-space formalizes this.
. Hyperplanes are very useful because they allows to separate the whole space in two regions. The notion of half-space formalizes this.
Example:
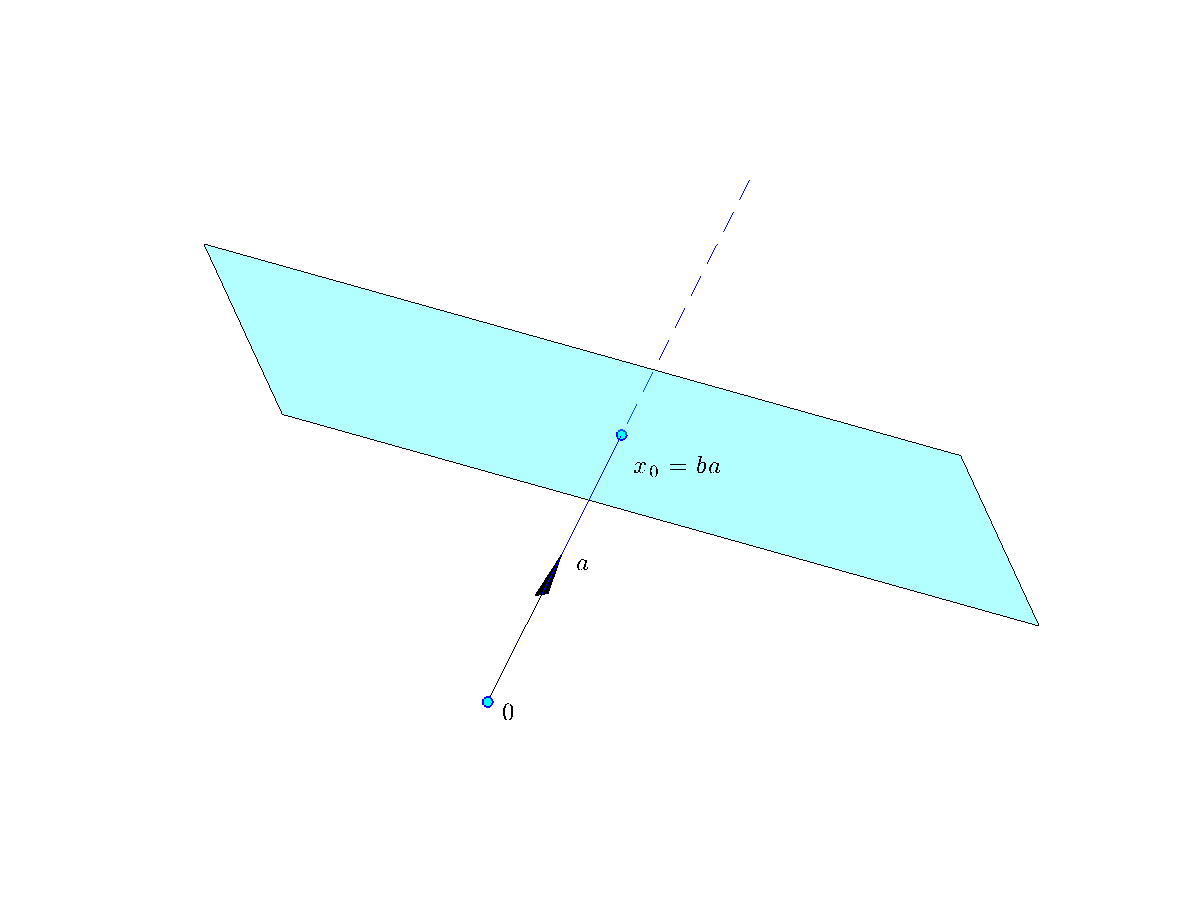
Projection on a hyperplane
Consider the hyperplane 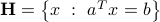 , and assume without loss of generality that
, and assume without loss of generality that  is normalized (
is normalized (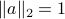 ). We can represent
). We can represent 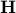 as the set of points
as the set of points  such that
such that 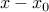 is orthogonal to
is orthogonal to  , where
, where 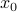 is any vector in
is any vector in  , that is, such that
, that is, such that 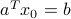 . One such vector is
. One such vector is 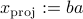 .
.
By construction, 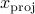 is the projection of
is the projection of  on
on 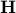 . That is, it is the point on
. That is, it is the point on 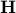 closest to the origin, as it solves the projection problem
closest to the origin, as it solves the projection problem
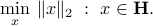
Indeed, for any 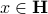 , using the Cauchy-Schwartz inequality:
, using the Cauchy-Schwartz inequality:
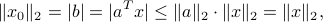
and the minimum length 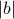 is attained with
is attained with 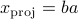 .
.
Geometry of hyperplanes
Half-spaces
A half-space is a subset of 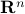 defined by a single inequality involving a scalar product. Precisely, an half-space in
defined by a single inequality involving a scalar product. Precisely, an half-space in 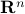 is a set of the form
is a set of the form
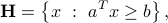
where 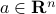 ,
, 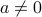 , and
, and 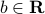 are given.
are given.
Geometrically, the half-space above is the set of points such that 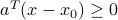 , that is, the angle between
, that is, the angle between 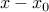 and
and  is acute (in
is acute (in ![[-90^circ, +90^circ]](eqs/5067945046856635014-130.png) ). Here
). Here 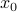 is the point closest to the origin on the hyperplane defined by the equality
is the point closest to the origin on the hyperplane defined by the equality 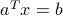 . (When
. (When  is normalized, as in the picture,
is normalized, as in the picture, 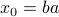 .)
.)
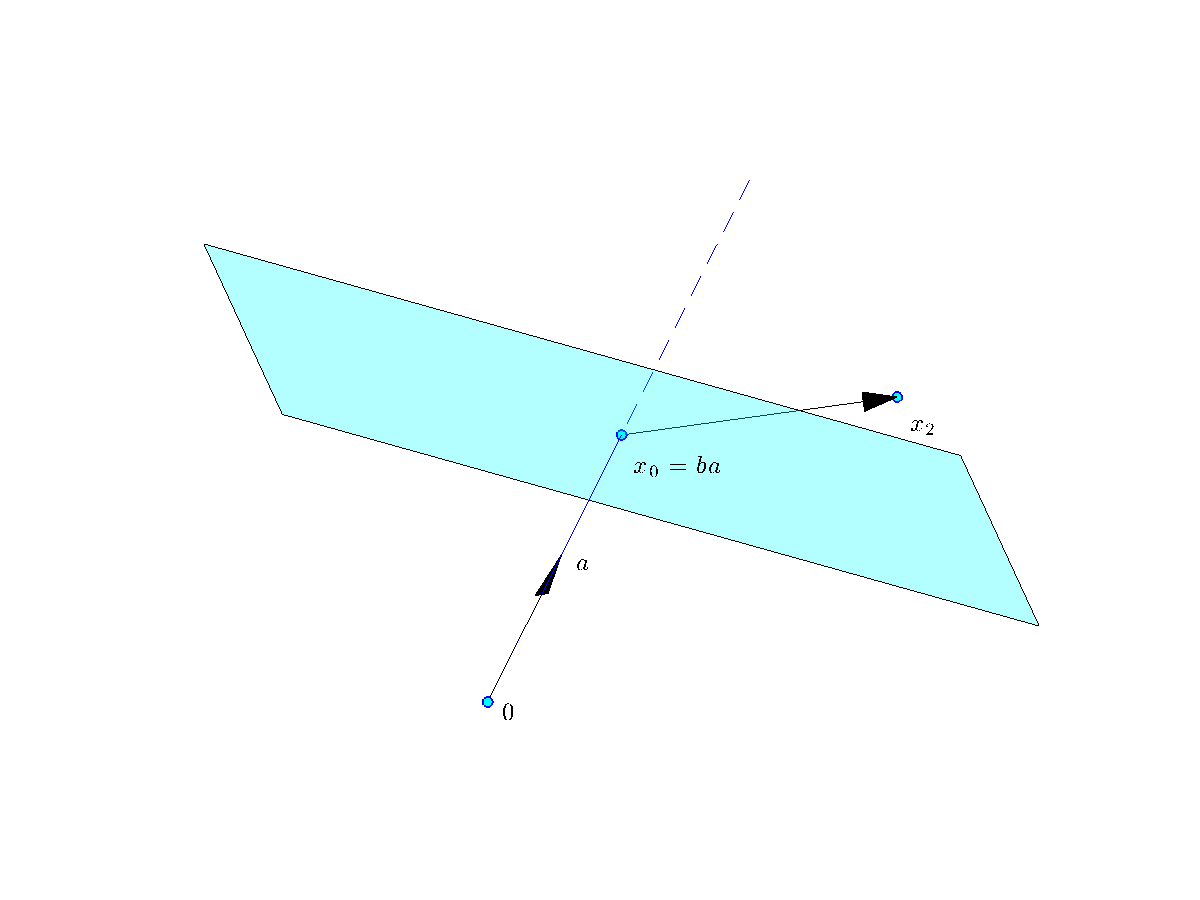 |
The half-space |
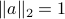 , is a translation of the set of vectors orthogonal to
, is a translation of the set of vectors orthogonal to 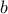 .
.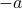 . As we increase the magnitude of
. As we increase the magnitude of 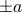 , depending on the sign of
, depending on the sign of 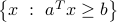 is the set of points such that
is the set of points such that