Projection on a line
Definition
Closed-form expression
Interpreting the scalar product
Definition
Consider the line in 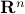 passing through
passing through 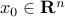 and with direction
and with direction 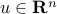 :
:
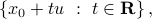
The projection of a given point  on the line is a vector
on the line is a vector  located on the line, that is closest to
located on the line, that is closest to  (in Euclidean norm). This corresponds to a simple optimization problem:
(in Euclidean norm). This corresponds to a simple optimization problem:
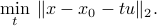
This particular problem is part of a general class of optimization problems known as least-squares. It is also a special case of a Euclidean projection on a general set.
Closed-form expression
Assuming that  is normalized, so that
is normalized, so that 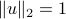 , the objecive function of the projection problem reads, after squaring:
, the objecive function of the projection problem reads, after squaring:
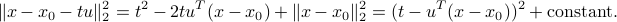
Thus, the optimal solution to the projection problem is
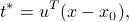
and the expression for the projected vector is
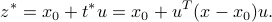
The scalar product 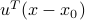 is the component of
is the component of 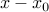 along
along  .
.
In the case when  is not normalized, the expression is obtained by replacing
is not normalized, the expression is obtained by replacing  with its scaled version
with its scaled version 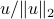 :
:
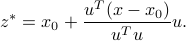
Interpreting the scalar product
We can now interpret the scalar product between two non-zero vectors 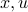 , by applying the previous derivation to the projection of
, by applying the previous derivation to the projection of  on the line of direction
on the line of direction  passing through the origin. If
passing through the origin. If  is normalized (
is normalized (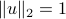 ), then the projection of
), then the projection of  on
on  is
is 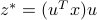 . Its length is
. Its length is 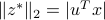 . (See above figure.)
. (See above figure.)
In general, the scalar product 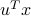 is simply the component of
is simply the component of  along the normalized direction
along the normalized direction 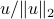 defined by
defined by  .
.
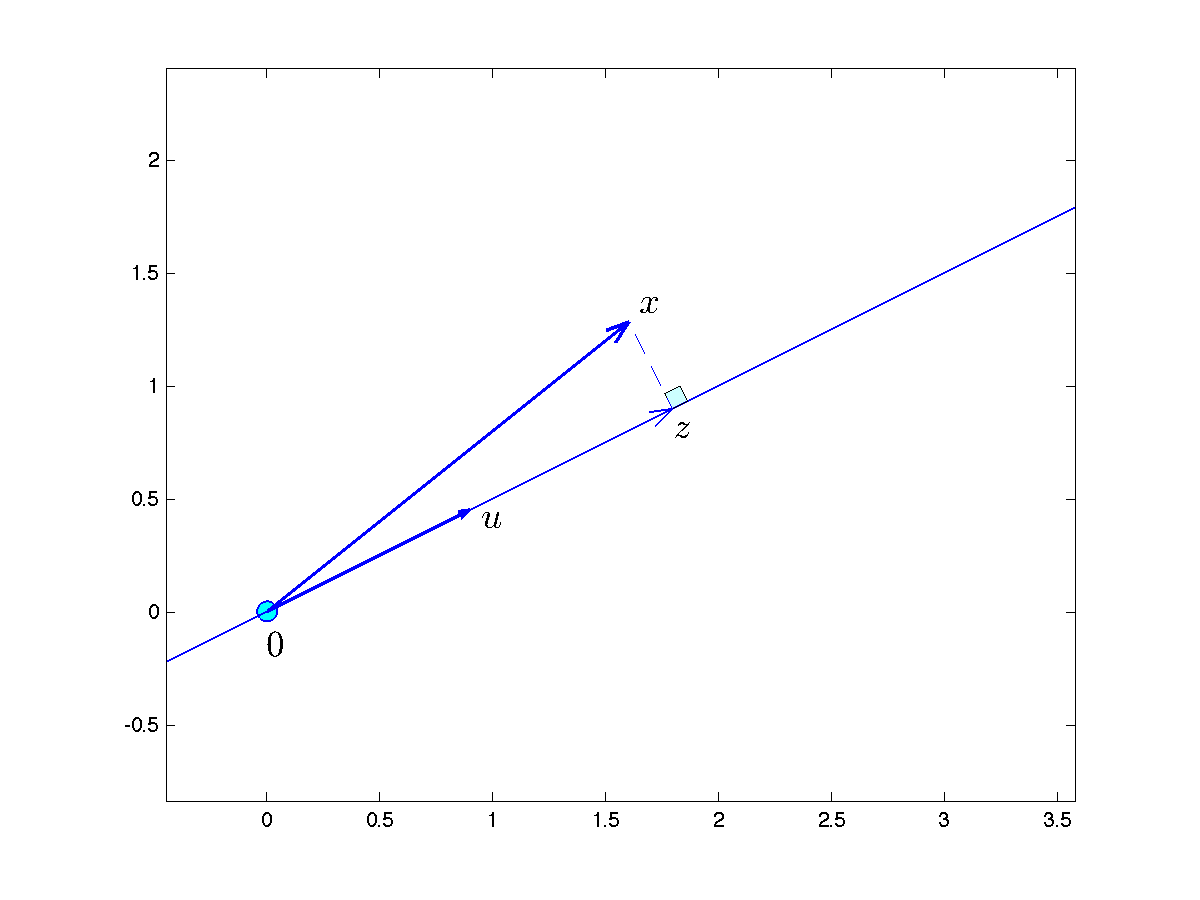
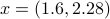 on a line passing through the origin (
on a line passing through the origin (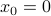 ) and with (normalized) direction
) and with (normalized) direction 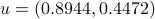 . At optimality the ‘‘residual’’ vector
. At optimality the ‘‘residual’’ vector  is orthogonal to the line, hence
is orthogonal to the line, hence 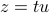 , with
, with 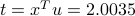 . Any other point on the line is farther away from the point
. Any other point on the line is farther away from the point 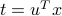 , ie the scalar product between
, ie the scalar product between