Some classes of optimization problems
Least-squares
Linear programming
Quadratic programming
Nonlinear optimization
Convex optimization
Combinatorial optimization
Least-squares
The least-squares problem is
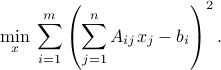
where 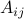 ,
, 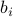 <
< 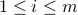 ,
, 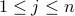 , are given numbers, and
, are given numbers, and  is the variable.
is the variable.
The problem was posed and solved by Gauss (1777-1855), who used the method it to predict the trajectory of the planetoid Ceres. Least-squares problems arise in many situations, for example in statistical estimation problems such as linear regression. In image compression this problem also arises, in which case 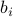 's contain a pixel representation of a given image, and for every
's contain a pixel representation of a given image, and for every 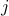 , the numbers
, the numbers 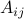 ,
, 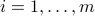 contain representations of ‘‘basic’’ images; the sums inside the squares represents a linear combination of these basic images that is supposed to approximate as well as possible the original image contained in
contain representations of ‘‘basic’’ images; the sums inside the squares represents a linear combination of these basic images that is supposed to approximate as well as possible the original image contained in 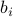 's.
's.
Example: linear regression via least-squares.
Linear programming
This problem is often referred to with the acronym LP, and has the form
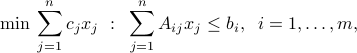
where 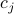 ,
, 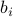 and
and 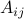 ,
, 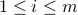 ,
, 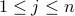 , are given real numbers. This corresponds to the case where the functions
, are given real numbers. This corresponds to the case where the functions 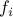 (
(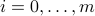 ) in the standard problem are all affine (that is, linear plus a constant term).
) in the standard problem are all affine (that is, linear plus a constant term).
This problem was introduced by G. Dantzig in the 40's in the context of logistical problems arising in military operations. This model of computation is perhaps the most widely used optimization problem today.
Example: Linear classification.
Quadratic programming
Quadratic programming problems (QP's for short) are an extension of linear programming, which involve a sum-of-squares function in the objective. The linear program above is modified to be
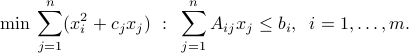
These problems can be thought of as a generalization of both the least-squares and linear programming problems.
QP's are popular in many areas, such as finance, where the linear term in the objective refers to the expected negative return on an investment, and the squared term corresponds to the risk (or variance of the return). This model was introduced in the 50's by H. Markowitz (who was then a colleague of Dantzig at the RAND Corporation), to model investment problems. Markowitz won the Nobel prize in Economics in 1990, mainly for this work.
Nonlinear optimization
Nonlinear optimization is perhaps the largest class of optimization problem. In general such problems are very hard to solve. ( In fact, this class comprises combinatorial optimization: if a variable 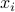 is required to be boolean, we can model this as a single non-linear constraint
is required to be boolean, we can model this as a single non-linear constraint 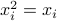 .)
.)
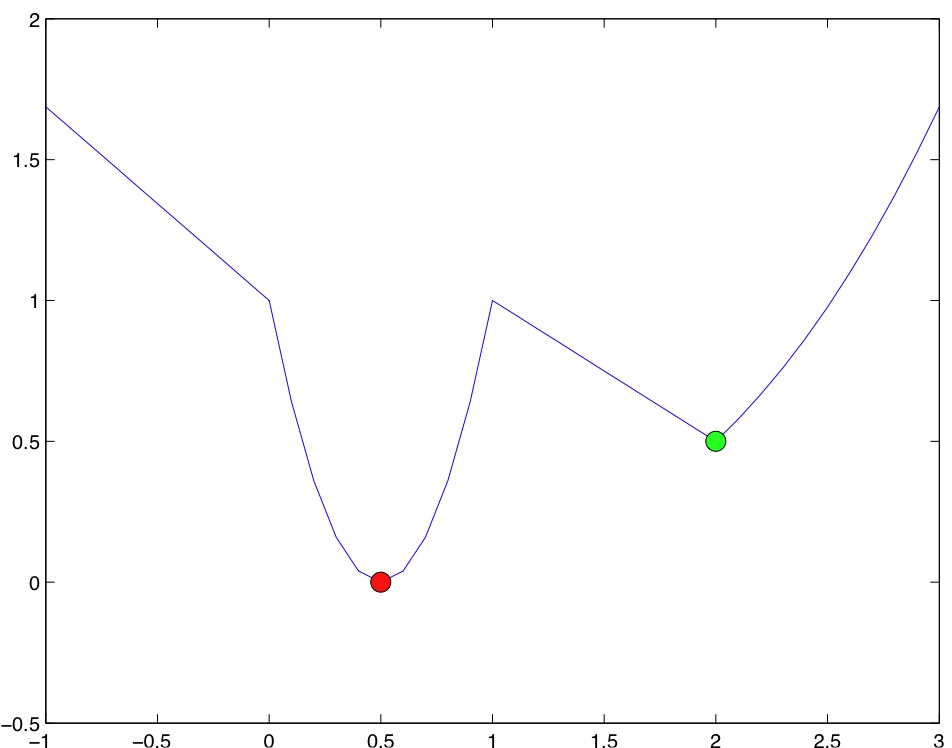
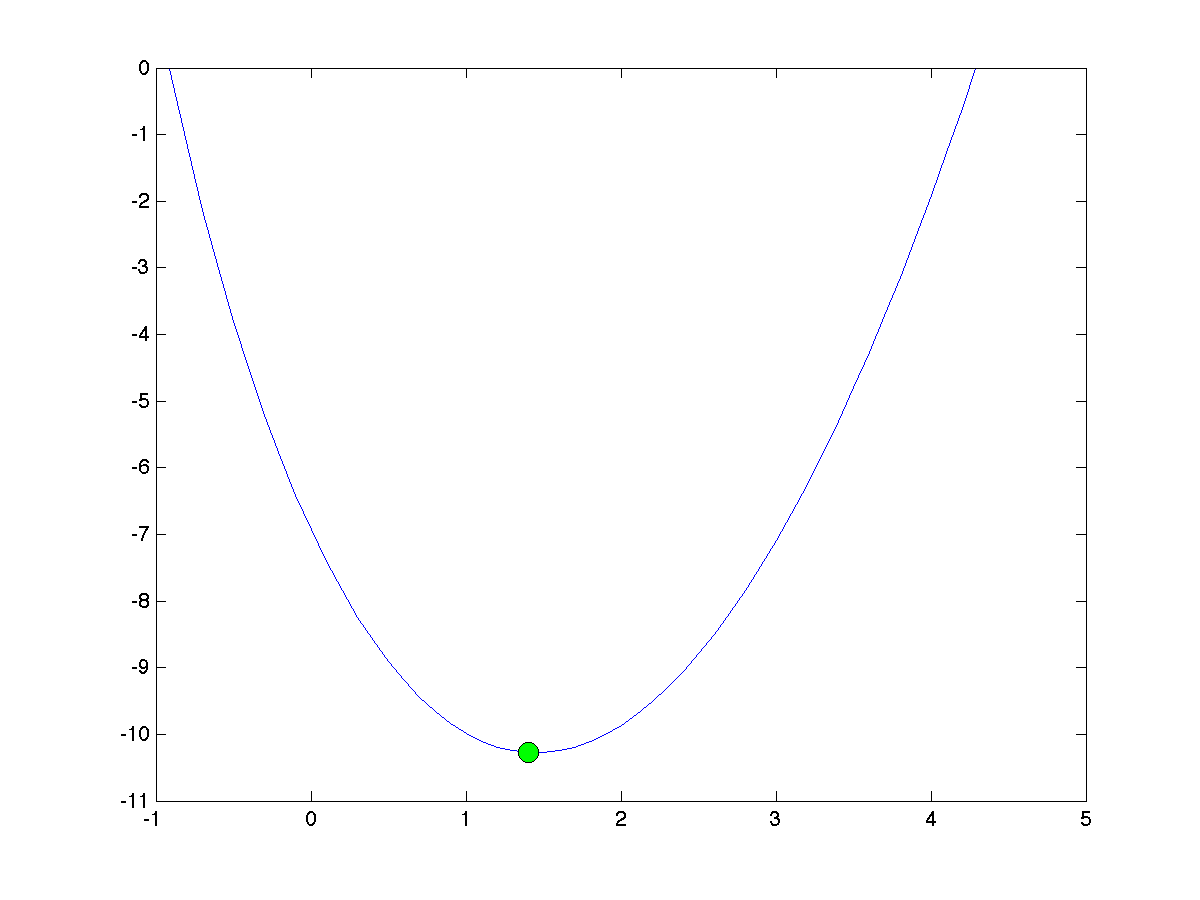
One of the reasons for which non-linear problems are hard to solve is the issue of local minima. We will define this notion rigorously, but the picture below provides an intuitive idea:
Example: Protein folding.
Convex optimization
Convex optimization is a generalization of QP where the objective and constraints involve ‘‘bowl-shaped’’, or convex, functions. Not all convex problems are easy to solve, but many of them are. One of the reasons for which this is (approximately) true is that, contrarily to general non-linear optimization problems, convex ones do not suffer from the ‘‘curse of local minima’’ mentioned above.
Combinatorial optimization
In combinatorial optimization, some (or all) the variables are boolean (or integers), reflecting discrete choices to be made.
Example: Crew allocation for airline operations.
Combinatorial optimization problems are in general extremely hard to solve. Often, they can be approximately solved with linear or convex programming.