Senate Voting: Projecting Data
Projection on a line
Projection on a plane
Projecting on a line
To simplify, let us first consider the simple problem of representing the high-dimensional data set on a simple line, using the method described here.
Scoring Senators
Specifically we would like to assign a single number, or ‘‘score’’, to each column of the matrix. We choose a direction 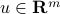 , and a scalar
, and a scalar 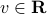 . This corresponds to the affine ‘‘scoring’’ function
. This corresponds to the affine ‘‘scoring’’ function 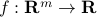 , which, to a generic column
, which, to a generic column 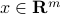 of the data matrix, assigns the value
of the data matrix, assigns the value
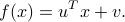
We thus obtain a vector of values 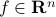 , with
, with 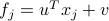 ,
, 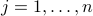 . It is often useful to center these values around zero. This can be done by choosing
. It is often useful to center these values around zero. This can be done by choosing  such that
such that
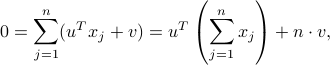
that is: 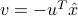 , where
, where
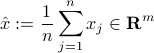
is the vector of sample averages across the columns of the matrix (that is, data points). The vector 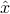 can be interpreted as the ‘‘average response’’ across experiments.
can be interpreted as the ‘‘average response’’ across experiments.
The values of our scoring function can now be expressed as
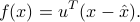
In order to be able to compare the relative merits of different directions, we can assume, without loss of generality, that the vector  is normalized (so that
is normalized (so that 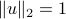 ).
).
Centering data
It is convenient to work with the ‘‘centered’’ data matrix, which is
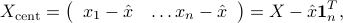
where 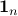 is the vector of ones in
is the vector of ones in 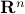 .
.
In matlab, we can compute the centered data matrix as follows.
>> xhat = mean(X,2); >> [m,n] = size(X); >> Xcent = X-xhat*ones(1,n);
We can compute the (row) vector scores using the simple matrix-vector product:

We can check that the average of the above row vector is zero:
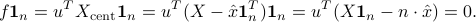
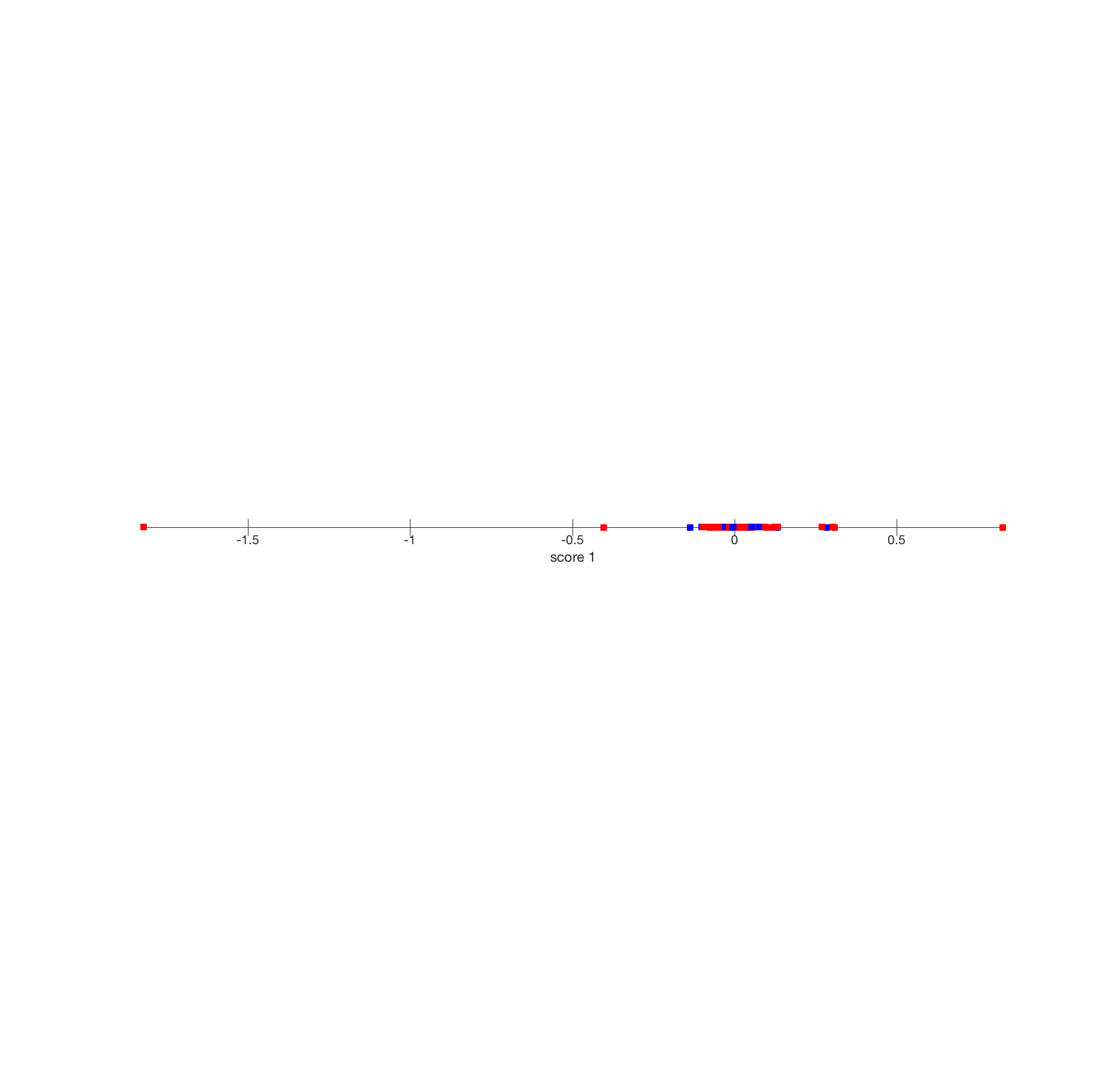
Example: visualizing along random direction
Projection on a plane
We can also try to project the data on a plane, which involves assigning two scores to each data point.
Scoring map
This corresponds to the affine ‘‘scoring’’ map 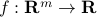 , which, to a generic column
, which, to a generic column 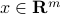 of the data matrix, assigns the two-dimensional value
of the data matrix, assigns the two-dimensional value
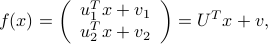
where 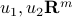 are two vectors, and
are two vectors, and 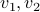 two scalars, while
two scalars, while ![U = [u_1,u_2]in mathbf{R}^{m times 2}](eqs/5329482852089801297-130.png) ,
, 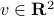 .
.
The affine map  allows to generate
allows to generate  two-dimensional data points (instead of
two-dimensional data points (instead of 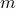 -dimensional)
-dimensional) 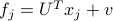 ,
, 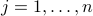 . As before, we can require that the
. As before, we can require that the 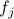 's be centered:
's be centered:
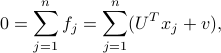
by choosing the vector  to be such that
to be such that 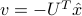 , where
, where 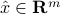 is the ‘‘average response’’ defined above. Our (centered) scoring map takes the form
is the ‘‘average response’’ defined above. Our (centered) scoring map takes the form
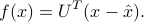
We can encapsulate the scores in the 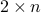 matrix
matrix ![F=[f_1,ldots,f_n]](eqs/2208268778030144376-130.png) . The latter can be expressed as the matrix-matrix product
. The latter can be expressed as the matrix-matrix product
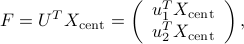
with 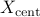 the centered data matrix defined above.
the centered data matrix defined above.
Clearly, depending on which plan we choose to project on, we get a very different pictures. Some planes seem to be more ‘‘informative’’ than others. We return to this issue here.
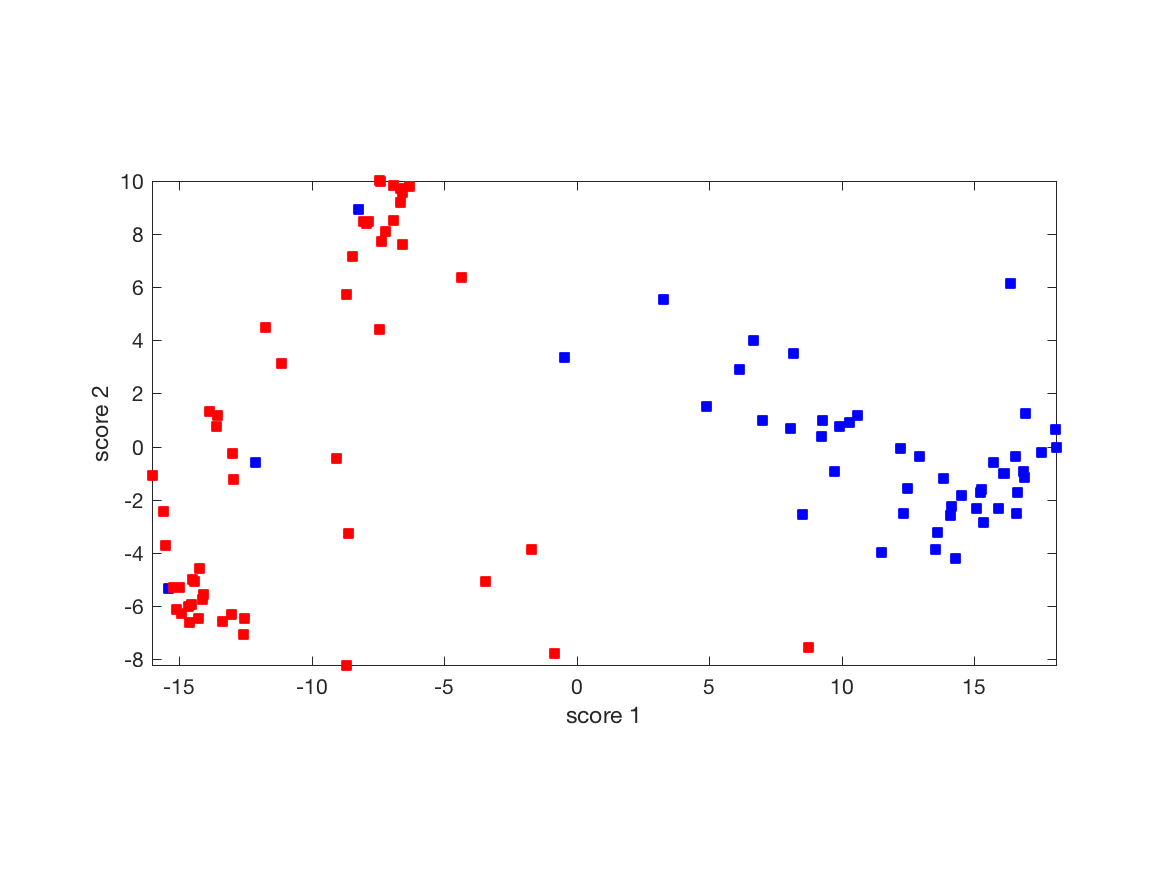 |
Two-dimensional projection of the Senate voting matrix: This particular projection seems to allow to cluster the Senators along party line, and is therefore more informative. We explain how choose such a direction here. |

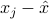 (that is, with average across Senators removed) on a (normalized) ‘‘random bill’’ direction. This projection shows no particular obvious structure. Note that the range of the data is much less than obtained with the average bill shown above.
(that is, with average across Senators removed) on a (normalized) ‘‘random bill’’ direction. This projection shows no particular obvious structure. Note that the range of the data is much less than obtained with the average bill shown above.