Minimum Surface Area
The minimum surface area problem
Discretization
SOCP formulation
The minimum surface area problem
Functional problem statement
Consider a surface in 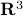 that is described by a function from the square
that is described by a function from the square ![C := [0,1] times [0,1]](eqs/5813364628852184551-130.png) to
to 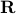 . The corresponding surface area is
. The corresponding surface area is

The minimum surface area problem is to find the function  which minimizes the area
which minimizes the area  , subject to boundary values. To be specific, we will assume that we are given values of
, subject to boundary values. To be specific, we will assume that we are given values of  on the left and right side of the square, that is
on the left and right side of the square, that is
![f(x,0) = l(x), ;; f(x,1) = r(x), ;; x in [0,1],](eqs/3429439964539566779-130.png)
where  and
and  are two given functions.
are two given functions.
The above is an infinite-dimensional problem, in the sense that the variable is a function, not a finite-dimensional vector.
Discretization
We can discretize the square with a square grid, with points  ,
,  , where
, where 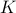 is an integer, and where
is an integer, and where  the (uniform) spacing of the grid. We represent the variable of our problem,
the (uniform) spacing of the grid. We represent the variable of our problem,  , as a matrix
, as a matrix  , with elements
, with elements  . Similarly, we represent the boundary conditions as vectors of length
. Similarly, we represent the boundary conditions as vectors of length 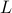 ,
, 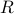 ,
,
To approximate the gradient, we start from the first-order expansion of a function of two variables, valid for some small increment 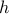 :
:

We obtain that the gradient of 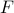 at a grid point can be approximated as
at a grid point can be approximated as

SOCP formulation
The discretized version of our problem is thus

The CVX syntax for this problem can be as follows.
>> % input: left_vals and righ_vals, two row vectors of length K+1
>> h = 1/K;
cvx_begin
variables F(K+1,K+1)
variables T(K,K)
minimize( sum(T(:)) )
subject to
for j = 1:K, for i = 1:K,
norm([K*(F(i+1,j)-F(i,j)); K*(F(i,j+1)-F(i,j)); 1],2) <= T(i,j);
end, end
F(1,:) == left_vals;
F(K+1,:) == right_vals;
cvx_end
Examples
 |
Minimal surface area joining two curves (in dark blue). |
It is interesting to compare the minimal surface area with one that is obtained by squaring the norms. This corresponds to the QP

