Total Variation Image Restoration
The image restoration problem
Discretization
SOCP formulation
The image restoration problem
Functional problem statement
Digital images always contain noise. In image restoration, the problem is to filter out the noise. Early methods involved least-squares but the solutions exhibited the ‘‘ringing’ phenomenon, with spurious oscillations near edges in the restored image. To address this phenomenon, one may add to the objective of the least-squares problem a term which penalizes the variations in the image.
We may represent a given (noisy) image as function from the square ![C := [0,1] times [0,1]](eqs/5813364628852184551-130.png) to
to 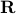 . We define the image restoration problem as minimizing, over functions
. We define the image restoration problem as minimizing, over functions  , the objective
, the objective

where the function  is our estimate. The first term penalizes functions which exhibit large variations, while the second term accounts for the distance from the estimate to the noisy image,
is our estimate. The first term penalizes functions which exhibit large variations, while the second term accounts for the distance from the estimate to the noisy image,  .
.
The above is an infinite-dimensional problem, in the sense that the variable is a function, not a finite-dimensional vector.
Discretization
We can discretize the square with a square grid, as follows:

We represent the data of our problem,  , as a matrix
, as a matrix  , with elements
, with elements  . Similarly, we represent the variable
. Similarly, we represent the variable  of our problem with a
of our problem with a  matrix
matrix  , which contains the values of
, which contains the values of  at the grid points
at the grid points  .
.
To approximate the gradient, we start from the first-order expansion of a function of two variables, valid for some small increment 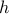 :
:

Applying this to a grid point, with the small increment set to  , we obtain that the gradient of
, we obtain that the gradient of  at a grid point can be approximated as
at a grid point can be approximated as

with the convention that the terms involved are zero on the boundary (that is, if either 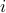 or
or 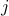 is
is  ).
).
SOCP formulation
The discretized version of our problem is thus
