Matrix Products
Matrix-vector product
Matrix-matrix product
Block matrix product
Trace and scalar product
Matrix-vector product
Definition
We define the matrix-vector product between a 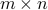 matrix and a
matrix and a  -vector
-vector  , and denote by
, and denote by 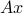 , the
, the 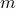 -vector with
-vector with 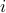 -th component
-th component
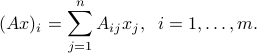
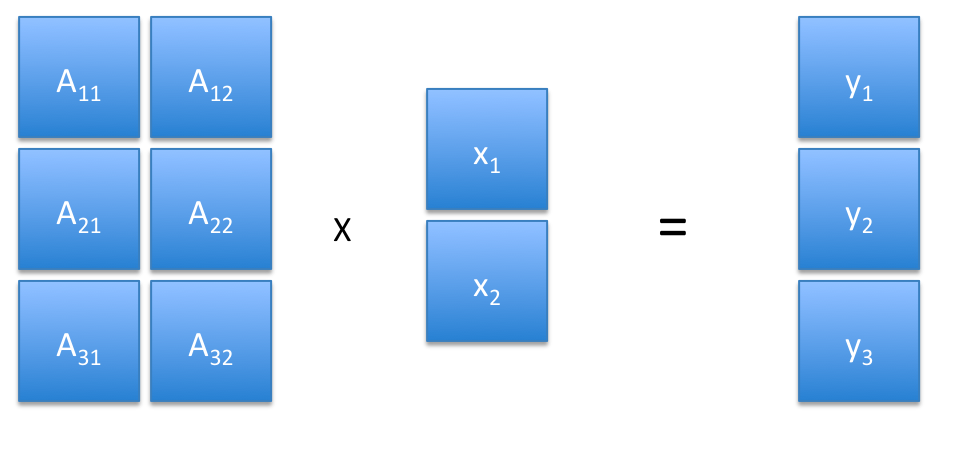 |
The picture on the left shows a symbolic example with 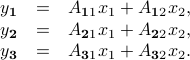
|
Interpretation as linear combinations of columns
If the columns of  are given by the vectors
are given by the vectors 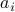 ,
, 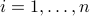 , so that
, so that 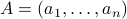 , then
, then 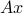 can be interpreted as a linear combination of these columns, with weights given by the vector
can be interpreted as a linear combination of these columns, with weights given by the vector  :
:
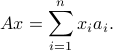
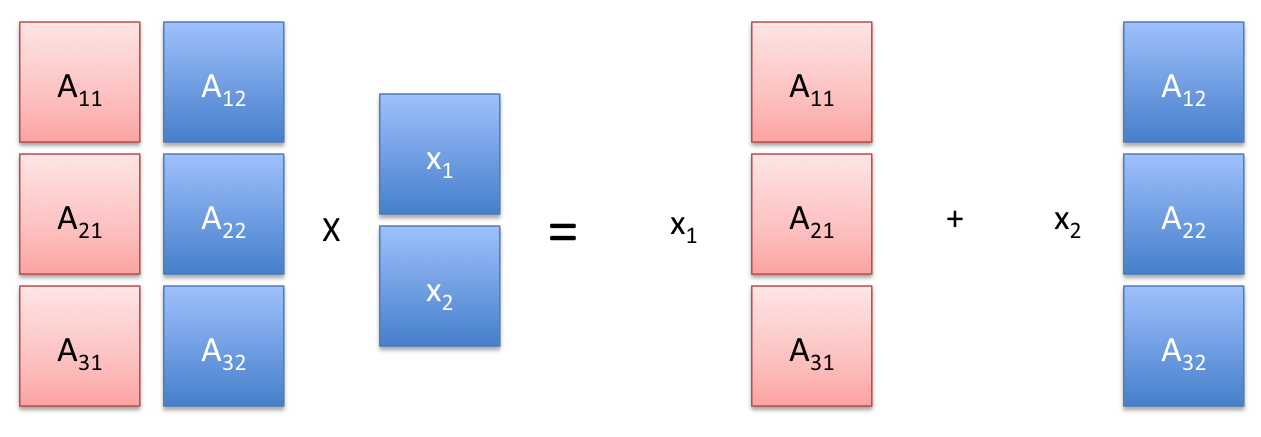 |
In the above symbolic example, we have 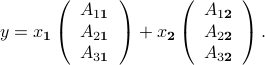
|
Example:
Interpretation as scalar products with rows
Alternatively, if the rows of  are the row vectors
are the row vectors 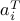 ,
, 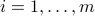 :
:
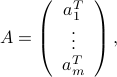
then 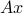 is the vector with elements
is the vector with elements 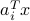 ,
, 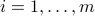 :
:
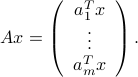
 |
In the above symbolic example, we have 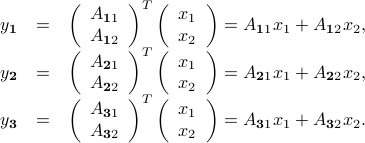
|
Example: Absorption spectrometry: using measurements at different light frequencies.
Left product
If 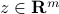 , then the notation
, then the notation 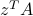 is the row vector of size
is the row vector of size  equal to the transpose of the column vector
equal to the transpose of the column vector 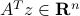 . That is:
. That is:
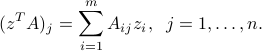
Example: Return to the network example, involving a 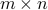 incidence matrix. We note that, by construction, the columns of
incidence matrix. We note that, by construction, the columns of  sum to zero, which can be compactly written as
sum to zero, which can be compactly written as 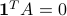 , or
, or 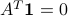 .
.
Matlab syntax
The product operator in Matlab is *. If the sizes are not consistent, Matlab will produce an error.
>> A = [1 2; 3 4; 5 6]; % 3x2 matrix >> x = [-1; 1]; % 2x1 vector >> y = A*x; % result is a 3x1 vector >> z = [-1; 0; 1]; % 3x1 vector >> y = z'*A; % result is a 1x2 (i.e., row) vector
Matrix-matrix product
Definition
We can extend matrix-vector product to matrix-matrix product, as follows. If 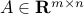 and
and 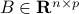 , the notation
, the notation 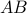 denotes the
denotes the 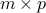 matrix with
matrix with 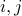 element given by
element given by
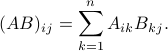
Transposing a product changes the order, so that 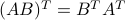 .
.
Column-wise interpretation
If the columns of 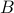 are given by the vectors
are given by the vectors 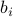 ,
, 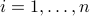 , so that
, so that ![B = [b_1 , ldots, b_n]](eqs/3204593958553039499-130.png) , then
, then 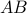 can be written as
can be written as
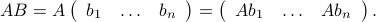
In other words, 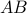 results from transforming each column
results from transforming each column 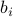 of
of 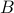 into
into 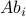 .
.
Row-wise interpretation
The matrix-matrix product can also be interpreted as an operation on the rows of  . Indeed, if
. Indeed, if  is given by its rows
is given by its rows 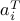 ,
, 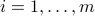 , then
, then 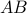 is the matrix obtained by transforming each one of these rows via
is the matrix obtained by transforming each one of these rows via 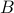 , into
, into 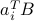 ,
, 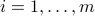 :
:
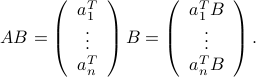
(Note that 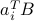 's are indeed row vectors, according to our matrix-vector rules.)
's are indeed row vectors, according to our matrix-vector rules.)
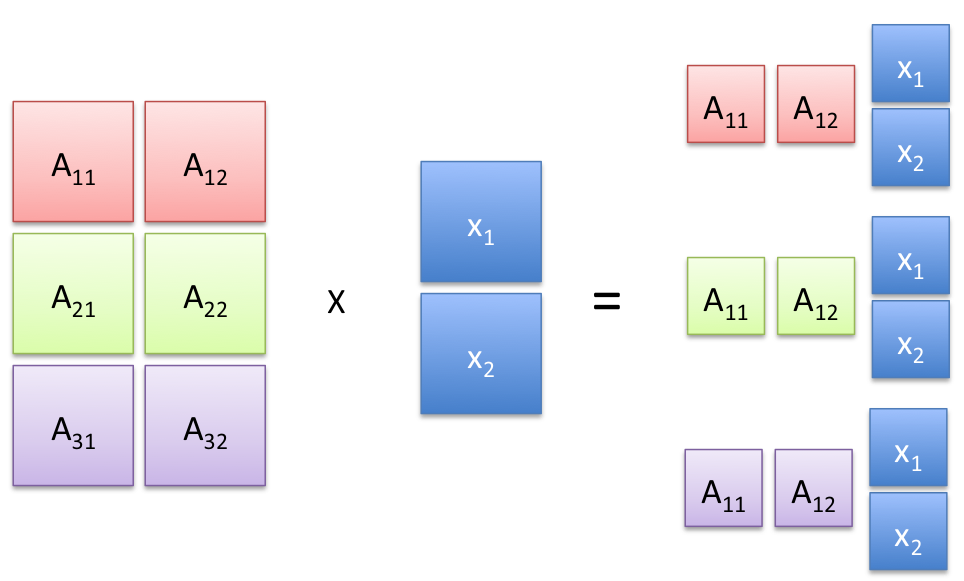
Block Matrix Products
Matrix algebra generalizes to blocks, provided block sizes are consistent. To illustrate this, consider the matrix-vector product between a  matrix
matrix  and a
and a  -vector
-vector  , where
, where  are partitioned in blocks, as follows:
are partitioned in blocks, as follows:
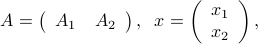
where 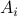 is
is 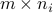 ,
, 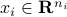 ,
, 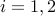 ,
, 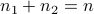 . Then
. Then
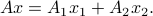
Symbolically, it's as if we would form the ‘‘scalar’’ product between the ‘‘row vector 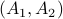 and the column vector
and the column vector 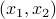 !
!
Likewise, if a 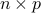 matrix
matrix 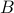 is partitioned into two blocks
is partitioned into two blocks 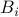 , each of size
, each of size 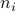 ,
, 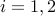 , with
, with 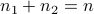 , then
, then
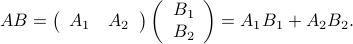
Again, symbolically we apply the same rules as for the scalar product — except that now the result is a matrix.
Example: Gram matrix.
Finally, we can consider so-called outer products. Consider the case for example when  is a
is a 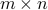 matrix partitioned row-wise into two blocks
matrix partitioned row-wise into two blocks 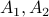 , and
, and 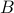 is a
is a 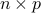 matrix that is partitioned column-wise into two blocks
matrix that is partitioned column-wise into two blocks 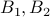 :
:
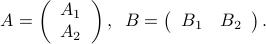
Then the product 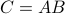 can be expressed in terms of the blocks, as follows:
can be expressed in terms of the blocks, as follows:
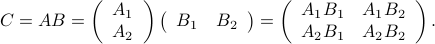
Trace, scalar product
Trace
The trace of a square 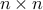 matrix
matrix  , denoted by
, denoted by 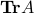 , is the sum of its diagonal elements:
, is the sum of its diagonal elements: 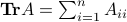 .
.
Some important properties:
Trace of transpose: The trace of a square matrix is equal to that of its transpose.
Commutativity under trace: for any two matrices
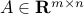 and
and 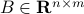 , we have
, we have
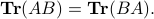
>> A = [1 2 3; 4 5 6; 7 8 9]; % 3x3 matrix >> tr = trace(A); % trace of A
Scalar product between matrices
We can define the scalar product between two 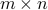 matrices
matrices 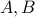 via
via
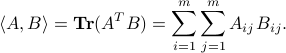
The above definition is symmetric: we have
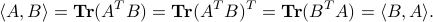
Our notation is consistent with the definition of the scalar product between two vectors, where we simply view a vector in  as a matrix in
as a matrix in  . We can interpret the matrix scalar product as the vector scalar product between two long vectors of length
. We can interpret the matrix scalar product as the vector scalar product between two long vectors of length 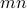 each, obtained by stacking all the columns of
each, obtained by stacking all the columns of 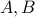 on top of each other.
on top of each other.
>> A = [1 2; 3 4; 5 6]; % 3x2 matrix
>> B = randn(3,2); % random 3x2 matrix
>> scal_prod = trace(A'*B); % scalar product between A and B
>> scal_prod = A(:)'*B(:); % this is the same as the scalar product between the
% vectorized forms of A, B
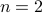 and
and 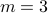 . We have
. We have 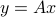 , that is:
, that is: