Boolean Quadratic Programming
Motivation: maximum cut (MAXCUT) problem
Boolean quadratic programming
Rank-constrained formulation
SDP relaxation
Sub-optimal solution via the SDP relaxation
Motivation: MAXCUT Problem
We consider an undirected graph with  nodes, described by its weight matrix
nodes, described by its weight matrix  , with
, with  the weight of the arc joining node
the weight of the arc joining node 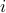 and
and 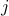 (with the convention that the weight is zero if there these nodes have no edge connecting them). The maximum cut problem is to find a partition of the nodes in two complementary groups, so that the total weight of the edges that connect the two groups is maximized.
(with the convention that the weight is zero if there these nodes have no edge connecting them). The maximum cut problem is to find a partition of the nodes in two complementary groups, so that the total weight of the edges that connect the two groups is maximized.
The max-cut problem can be formalized via the following boolean quadratic problem:

Here, the boolean variable  corresponds to a particular assignement of each node into one of the two groups. The constraints in the above problem enforce the Boolean conditions on
corresponds to a particular assignement of each node into one of the two groups. The constraints in the above problem enforce the Boolean conditions on  . We check that the term
. We check that the term  is zero if and only if
is zero if and only if 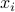 and
and 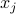 are equal, which means that node
are equal, which means that node 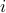 and node
and node 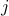 are in the same group; otherwise, the cost is
are in the same group; otherwise, the cost is  .
.
Boolean QP
The above problem falls into the more general class of Boolean quadratic programs, which are of the form

where  , with
, with  of arbitrary sign. Boolean QPs, as well as the special case of max-cut problems, are combinatorial, and hard to solve exactly. However, theory (based on SDP relaxations seen below) says that we can approximate the above quantity with a relative error of at most
of arbitrary sign. Boolean QPs, as well as the special case of max-cut problems, are combinatorial, and hard to solve exactly. However, theory (based on SDP relaxations seen below) says that we can approximate the above quantity with a relative error of at most  (the number falls to
(the number falls to  in the case of MAX-CUT, which has special structure).
in the case of MAX-CUT, which has special structure).
Rank-Constrained Formulation
We will introduce a semidefinite approximation to the problem, which is based on an expression of the original Boolean QP in terms of a matrix variable  , with components
, with components
 ,
,  . We can write the relationship between the vector
. We can write the relationship between the vector  and the matrix
and the matrix 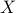 more compactly, as
more compactly, as

We observe that 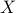 is positive semi-definite by construction.
is positive semi-definite by construction.
We note that the objective of the Boolean QP, while quadratic in the original decision vector  , is actually linear in the matrix
, is actually linear in the matrix 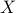 , since
, since

The same is true of the constraints:

Finally, we note that a given symmetric matrix 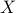 has the form
has the form  for some vector
for some vector  if and only if it is positive semi-definite and its rank is one.
if and only if it is positive semi-definite and its rank is one.
This means that we can formulate the Boolean QP in an equivalent, ’'rank-constrained’’ form:

Semidefinite Relaxation
The above rank-constrained problem is not convex, precisely due to the rank constraint. If we remove the constraint, we do obtain a convex problem — in fact, an SDP. This SDP is a relaxation of the original problem, that is, it is a new problem obtained by removing constraints. Since we are maximizing, the new problem yields an upper bound on the original one:

We can check that indeed the problem of computing  is an SDP:
is an SDP:
it involves a matrix variable that is constrained to the positive semi-definite cone;
the other constraints are affine;
the objective is linear.
The gap between 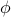 (the true value of the combinatorial problem) and
(the true value of the combinatorial problem) and  (the SDP approximation) can be large, but not arbitrarily so. In fact, as mentioned above, it has been shown (by Nesterov in 1996) that the relative error satisfies
(the SDP approximation) can be large, but not arbitrarily so. In fact, as mentioned above, it has been shown (by Nesterov in 1996) that the relative error satisfies

independent of problem size (and of data matrix  ).
).